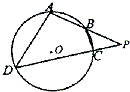
摘要：4． 四边形PMNQ为⊙O的内接梯形.圆心O在MN上.向量与的夹角为150°. (1)求⊙O的方程 (2)求以M.N为焦点且过P.Q两点的椭圆方程 (1)以MN所在直线为x轴.MN的中垂线为y轴建立如图所示的直角坐标系 ∵ 与夹角为150°.∴ 与夹角为30° ∴∠QMN=∠QPN=30°.∴∠OQM=∠OMQ=30° 设⊙O的半径为R.则QM= ∵ ∴ ∴R2=4 ∴⊙O方程为x2+y2=4 (2)∠QON=60° ∴Q 即Q(1.).∴P(-1.) 设所求椭圆方程为 ∵其焦点坐标为.点P.Q在椭圆上 ∴ ∴ ∴椭圆方程为

网址：http://m.1010jiajiao.com/timu3_id_531939[举报]