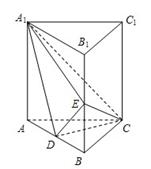
摘要:证明:(Ⅰ) 直棱柱中.BB1⊥平面ABCD.BB1⊥AC. 又∠BAD=∠ADC=90°..∴.∠CAB=45°.∴. BC⊥AC.又.平面BB1C1C. AC⊥平面BB1C1C. (Ⅱ)存在点P.P为A1B1的中点.证明:由P为A1B1的中点.有PB1|AB.且PB1=AB. 又∵DC|AB.DC=AB.DC ∥PB1.且DC= PB1. ∴DC PB1为平行四边形.从而CB1∥DP.分 又CB1面ACB1.DP 面ACB1.DP|面ACB1. 同理.DP|面BCB1.
网址:http://m.1010jiajiao.com/timu3_id_531815[举报]
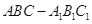 中,
中,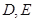 分别是
分别是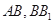 的中点,
的中点,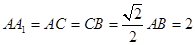 .
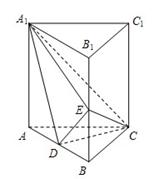
.
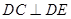 ;
;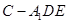 的体积.
的体积. 中,
中,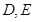 分别是
分别是 的中点,
的中点,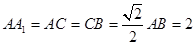 .
.
 ;
;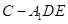 的体积.
的体积.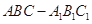 中,
中,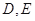 分别是
分别是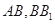 的中点,
的中点, .
.
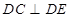 ;
;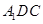 所成角的正弦值.
所成角的正弦值.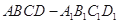 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, .
.
 平面
平面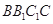 ;
; ,使得
,使得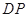 与平面
与平面 平行?证明你的结论.
平行?证明你的结论.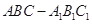 中,
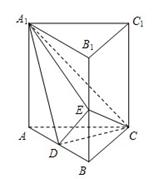
中,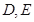 分别是
分别是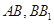 的中点,
的中点,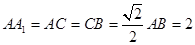 .
.
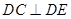 ;
;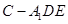 的体积.
的体积.