摘要:2.设数列满足.若是等差数列.是等比数列. (1)分别求出数列的通项公式,(2)求数列中最小项及最小项的值, (3)是否存在.使.若存在.求满足条件的所有值,若不存在.请说明理由. 解:(1)由成等差数列知其公差为1. 故 由等比数列知.其公比为.故 = +6== =+6=2+ 题知,= ,所以当或时.取最小项.其值为3 (3)假设存在.使-2-=- 则- 即 ∵是相邻整数 ∴.这与矛盾.所以满足条件的不存在
网址:http://m.1010jiajiao.com/timu3_id_531790[举报]
 满足
满足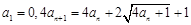 ,令
,令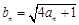 .
. 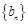 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;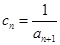 ,求
,求 前
前 项的和
项的和 ;
;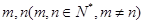 使得
使得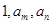 三数成等比数列?
三数成等比数列?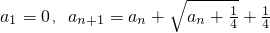 ,令
,令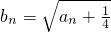 .
. ,令
,令 .
.