题目内容
设数列 满足
满足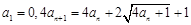 ,令
,令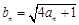 .
.
(1)试判断数列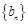 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;
(2)若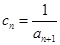 ,求
,求 前
前 项的和
项的和 ;
;
(3)是否存在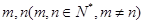 使得
使得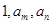 三数成等比数列?
三数成等比数列?
(1)数列 为等差数列;(2)
为等差数列;(2)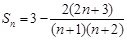 ;(3)不存在
;(3)不存在
解析试题分析:(1)由已知可变形为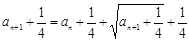 即
即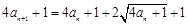 ,所以
,所以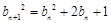 ,即
,即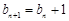 ,所以数列
,所以数列 为等差数列;(2)由⑴得
为等差数列;(2)由⑴得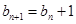 且
且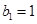 ,
,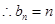 ,
,
所以 ,从而
,从而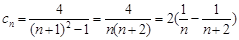 ,裂项相消求得
,裂项相消求得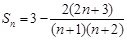 ;(3)设存在
;(3)设存在 满足条件,则有
满足条件,则有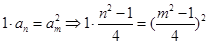 即
即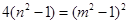 ,所以,
,所以,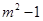 必为偶数,设为
必为偶数,设为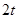 ,则
,则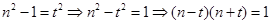 ,有
,有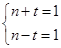 或
或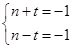 ,即
,即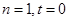 ,
,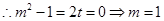 与已知矛盾,故不存在
与已知矛盾,故不存在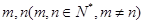 使得
使得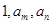 三数成等比数列.
三数成等比数列.
试题解析:⑴由已知得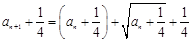 , 即
, 即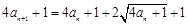 ,
,
所以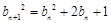 ,即
,即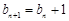 ,
,
所以数列 为等差数列;
为等差数列;
⑵由⑴得: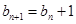 且
且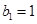 ,
,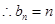 ,
,
即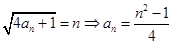 ,
,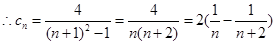 ,
,
则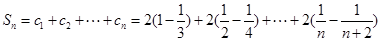
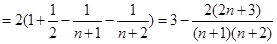 ;
;
⑶设存在 满足条件,则有
满足条件,则有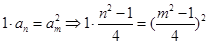 ,
,
即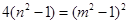 ,所以,
,所以,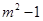 必为偶数,设为
必为偶数,设为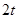 ,
,
则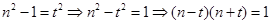 ,
, 有
有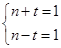 或
或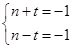 ,即
,即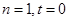 ,
, 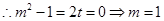 与已知矛盾.
与已知矛盾. 不存在
不存在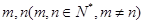 使得
使得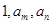 三数成等比数列.
三数成等比数列.
考点:等差数列的定义

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
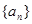 成等差数列,其前
成等差数列,其前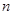 项和为
项和为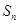 ,若
,若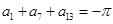 ,则
,则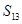 的余弦值为 .
的余弦值为 .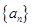 中,
中,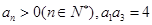 ,且
,且 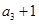 是
是  和
和 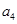 的等差中项,若
的等差中项,若 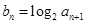
 的通项公式;
的通项公式;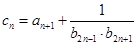 ,求数列
,求数列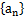 满足:
满足: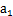 =2,且
=2,且 成等比数列.
成等比数列.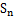 为数列
为数列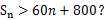 若存在,求n的最小值;若不存在,说明理由.
若存在,求n的最小值;若不存在,说明理由.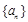 中,
中,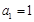 ,且
,且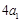 ,
, ,
,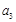 成等差数列.
成等差数列.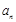 ;
; ,求数列
,求数列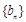 的前
的前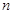 项和
项和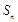 .
.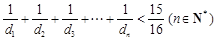 .
.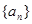 中,已知
中,已知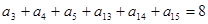 ,则
,则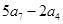 = .
= .