摘要: 设是定义在上的函数.且满足:①对任意.恒有>0,②对任意.恒有,则关于函数有 ⑴对任意.都有, ⑵对任意.都有, ⑶对任意.都有,⑷对任意.都有 上述四个命题中正确的有 (见思想方法专题)赋值法
网址:http://m.1010jiajiao.com/timu3_id_531107[举报]
设函数![]() 是定义在
是定义在![]() 上的函数,并且满足下面三个条件:(1)对正数x、y都有
上的函数,并且满足下面三个条件:(1)对正数x、y都有![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)
;(3)![]() 。则
。则
(Ⅰ)求![]() 和
和![]() 的值;
的值;
(Ⅱ)如果不等式![]() 成立,求x的取值范围.
成立,求x的取值范围.
(Ⅲ)如果存在正数k,使不等式![]() 有解,求正数
有解,求正数![]() 的取值范围.
的取值范围.
设函数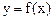 是定义在
是定义在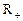 上的函数,并且满足下面三个条件:(1)对正数x、y都有
上的函数,并且满足下面三个条件:(1)对正数x、y都有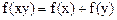 ;(2)当
;(2)当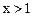 时,
时,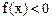 ;(3)
;(3)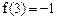 。则
。则
(Ⅰ)求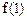 和
和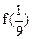 的值;
的值;
(Ⅱ)如果不等式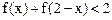 成立,求x的取值范围.
成立,求x的取值范围.
(Ⅲ)如果存在正数k,使不等式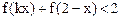 有解,求正数
有解,求正数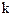 的取值范围.
的取值范围.
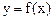 是定义在
是定义在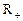 上的函数,并且满足下面三个条件:(1)对正数x、y都有
上的函数,并且满足下面三个条件:(1)对正数x、y都有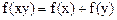 ;(2)当
;(2)当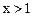 时,
时,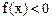 ;(3)
;(3)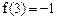 。则
。则(Ⅰ)求
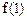 和
和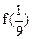 的值;
的值;(Ⅱ)如果不等式
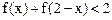 成立,求x的取值范围.
成立,求x的取值范围.(Ⅲ)如果存在正数k,使不等式
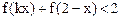 有解,求正数
有解,求正数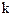 的取值范围.
的取值范围.设 是定义在R上的偶函数,满足
是定义在R上的偶函数,满足 ,且在[-1,0]上是增函数,给出下列关于函数
,且在[-1,0]上是增函数,给出下列关于函数 的判断:①
的判断:① 是周期函数;②
是周期函数;② 的图像关于直线x=1对称;③
的图像关于直线x=1对称;③ 在[0,1]上是增函数;其中所有正确判断的序号是 。
在[0,1]上是增函数;其中所有正确判断的序号是 。
查看习题详情和答案>>
A是定义在[2,4]上且满足如下两个条件的函数Φ(x)组成的集合:
①对任意的x∈[1,2],都有Φ(2x)∈(1,2);
②存在常数L(0<L<1),使得对任意的x1,x2∈[1,2],都有|Φ(2x1)-Φ(2x2)|≤L|x1-x2|;
(1)设Φ(x)=
3]1+x,x∈[2,4],证明:Φ(x)∈A;
(2)设Φ(x)∈A,如果存在x0∈(1,2),使得x0=Φ(2x0),那么,这样的x0是唯一的;
(3)设Φ(x)∈A,任取x1∈(1,2),令xn+1=Φ(2xn),n=1,2,…,
证明:给定正整数k,对任意的正整数p,不等式|xk+p-xk|≤
|x2-x1|成立.
查看习题详情和答案>>
①对任意的x∈[1,2],都有Φ(2x)∈(1,2);
②存在常数L(0<L<1),使得对任意的x1,x2∈[1,2],都有|Φ(2x1)-Φ(2x2)|≤L|x1-x2|;
(1)设Φ(x)=
| [ |
(2)设Φ(x)∈A,如果存在x0∈(1,2),使得x0=Φ(2x0),那么,这样的x0是唯一的;
(3)设Φ(x)∈A,任取x1∈(1,2),令xn+1=Φ(2xn),n=1,2,…,
证明:给定正整数k,对任意的正整数p,不等式|xk+p-xk|≤
| Lk-1 |
| 1-L |