摘要:21.已知函数时.函数取得极大值. (I)求实数的值, (Ⅱ)若函数在区间内导数都存在.且.则存在 .使得.无需证明即可利用上述结论 证明:若.则对任意 都有, (Ⅲ)已知正数满足求证:当时.对任 意大于-1.且互不相等的实数.-.,都有 -+. 请考生在第22.23.24题中任选一题做答.如果多做.那么按所组的第一题记分. 做答时.用2B铅笔在答题卡上把所选题目对应的题号涂黑.
网址:http://m.1010jiajiao.com/timu3_id_530067[举报]
(本小题满分12分) 已知函数![]() 的图象与x、y轴分别相交于点A、B,
的图象与x、y轴分别相交于点A、B,![]() (
(![]() 、
、![]() 分别是与x、y轴正半轴同方向的单位向量), 函数
分别是与x、y轴正半轴同方向的单位向量), 函数![]() .
.
(Ⅰ) 求k、b的值;
(Ⅱ) 当x满足![]() 时,求不等式
时,求不等式![]() 恒成立时
恒成立时![]() 的取值范围.
的取值范围.
(本小题满分12分) 已知函数![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上为减函数.
上为减函数.
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)若当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(Ⅲ)是否存在实数![]() 使得关于
使得关于![]() 的方程
的方程![]() 在区间[0,2]上恰好有两个相异的实根,若存在,求实数
在区间[0,2]上恰好有两个相异的实根,若存在,求实数![]() 的取值范围.
的取值范围.
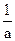 时,f(
时,f(