题目内容
本小题满分12分)
已知函数f(x)=lnx-ax2+(2-a)x.
(I)讨论f(x)的单调性;
(II)设a>0,证明:当0<x<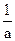 时,f(
时,f(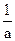 +x)>f(
+x)>f(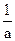 -x);
-x);
(III)若函数y=f(x)的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f’( x0)<0.
解析:(I)f(x)的定义域为(0,+∞),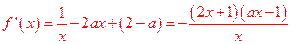 ,
,
①若a≤0,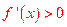 ,所以f(x)在(0,+∞)单调增加;
,所以f(x)在(0,+∞)单调增加;
②若a>0,则由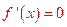 得
得
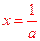 ,且当
,且当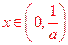 时,
时,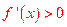 ,当
,当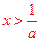 时,
时,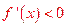 ,所以f(x)在
,所以f(x)在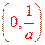 单调增加,在
单调增加,在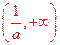 单调
单调 减少.
减少.
(II)设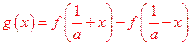 ,则
,则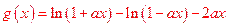 ,
,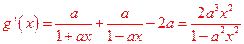 ,
,
当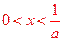 时,
时,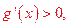 而
而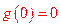 ,所以
,所以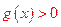 .
.
故当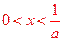 时,
时, 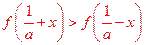

解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,记函数
,记函数 ,
, 的最小正周期为
的最小正周期为 .
.  的值;
的值; 时,试求
时,试求 上的单调递增区间.
上的单调递增区间.
 是椭圆上纵坐标不为零的两点,若
是椭圆上纵坐标不为零的两点,若 其中F为椭圆的左焦点.
其中F为椭圆的左焦点. 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于
 (
( )两点,且
)两点,且 .
. 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若 ,求
,求 的值.
的值. ,
, ,
, ,求实数
,求实数 的值;
的值; ,求实数
,求实数 ,且对于任意实数
,且对于任意实数 ,恒有
,恒有 .
. 的解析式;
的解析式;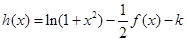 有几个零点?
有几个零点?