题目内容
已知函数 其中a>0.
其中a>0.
(I)求函数f(x)的单调区间;
(II)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围;
(III)当a=1时,设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间[-3,-1]上的最小值。
【考点定位】本小题主要考查导数的运算,利用导数研究函数的单调性、函数的零点,函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.
【答案】
(I)单调递增区间是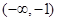 ,
,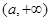 ;单调递减区间是
;单调递减区间是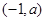 (2)
(2)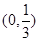
(3)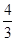
【解析】(I)解: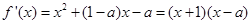
由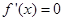 ,得
,得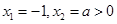
当x变化时,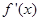 ,
,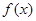 的变化情况如下表:
的变化情况如下表:
|
x |
|
-1 |
|
a |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故函数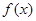 的单调递增区间是
的单调递增区间是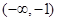 ,
,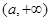 ;单调递减区间是
;单调递减区间是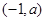 .
.
(II)解:由(I)知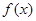 在区间
在区间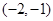 内单调递增,在
内单调递增,在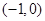 内单调递减,从而函数
内单调递减,从而函数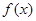 在区间
在区间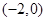 内恰有两个零点当且仅当
内恰有两个零点当且仅当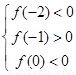 ,解得
,解得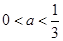 .
.
所以,a的取值范围是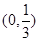 .
.
(III)解:a=1时,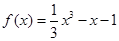 .由(I)知
.由(I)知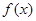 在区间
在区间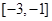 内单调递增,在
内单调递增,在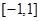 内单调递减,在
内单调递减,在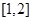 上单调递增.
上单调递增.
(1)当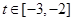 时,
时,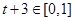 ,
,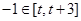 ,
,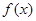 在
在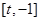 上单调递增,在
上单调递增,在 上单调递减.因此,
上单调递减.因此,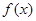 在
在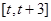 上的最大值
上的最大值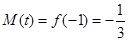 ,而最小值
,而最小值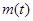 为
为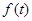 与
与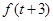 中的较小者.由
中的较小者.由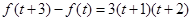 知,当
知,当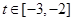 时,
时,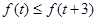 ,故
,故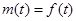 ,所以
,所以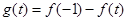 .而
.而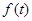 在
在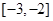 上单调递增,因此
上单调递增,因此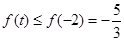 .所以
.所以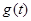 在
在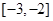 上的最小值为
上的最小值为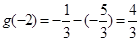 .
.
(2)当 时,
时,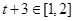 ,且
,且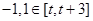 .
.
下面比较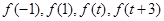 的大小由
的大小由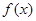 在
在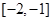 ,
,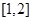 上单调递增,
上单调递增,
有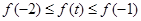
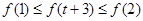
又由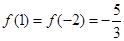 ,
,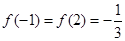 ,
,
从而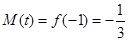 ,
,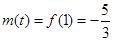
所以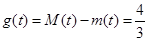 综上,函数
综上,函数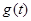 在区间
在区间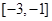 上的最小值为
上的最小值为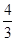

练习册系列答案
相关题目
 其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域; ;
; 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
 (其中A>0,
(其中A>0, )的图象如图所示.
)的图象如图所示. ,求
,求 的值.
的值.
 其中a>0,e为自然对数的底数。
其中a>0,e为自然对数的底数。
 的单调区间;
的单调区间;