摘要：20． 解:(1)由题意得: . ---------4分 所以椭圆的方程为 ----------------6分 (2)由题可知当直线PA过圆M的圆心(8.6)时.弦PQ最大. --8分 因为直线PA的斜率一定存在.设直线PA的方程为:y-6=k(x-8) --10分 又因为PA与圆O相切.所以圆心(0.0)到直线PA的距离为 --11分 即 可得 --------12分 所以直线PA的方程为: ----14分
网址：http://m.1010jiajiao.com/timu3_id_528960[举报]
（本小题满分14分）
已知：函数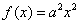
（
），
．
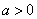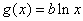（1）若函数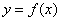
图象上的点到直线
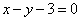距离的最小值为
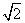，求
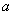的值；
（2）关于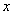
的不等式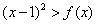
的解集中的整数恰有3个，求实数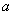的取值范围；
（3）对于函数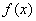
与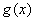
定义域上的任意实数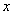，若存在常数
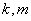，使得不等式
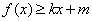和
都成立，则称直线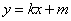
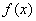为函数与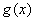的“分界线”。设
，
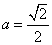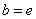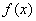，试探究与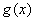是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
查看习题详情和答案>>
（本小题满分14分）
设数列
是公差为
的等差数列，其前
项和为
．
（1）已知
，
，
（ⅰ）求当
时，
的最小值；
（ⅱ）当时，求证：
；
（2）是否存在实数
，使得对任意正整数，关于
的不等式
的最小正整数解为
?若存在，则求的取值范围；若不存在，则说明理由．
（本小题满分14分）
设数列
是公差为
的等差数列，其前
项和为
．
（1）已知
，
，
（ⅰ）求当
时，
的最小值；
（ⅱ）当时，求证：
；
（2）是否存在实数
，使得对任意正整数，关于
的不等式
的最小正整数解为
?若存在，则求的取值范围；若不存在，则说明理由．