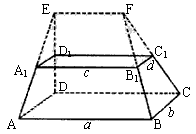
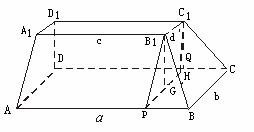
摘要:估算法: 如图.在多面体ABCDEF中.已知面ABCD是边长为3的正方形.EF//AB. EF=3/2.EF与面AC的距离为2.则该多面体的体积为( ) A)9/2 B)5 C)6 D)15/2
网址:http://m.1010jiajiao.com/timu3_id_528801[举报]
(02年北京卷文)(12分)
如图,在多面体ABCD―A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,上、下底面矩形的长、宽分别为c,d与a,b且a>c,b>d,两底面间的距离为h..
(Ⅰ)求侧面ABB1A1与底面ABCD所成二面角正切值;
(Ⅱ)在估测该多面体的体积时,经常运用近似公式
V估=S中截面?h来计算.已知它的体积公式是
![]() (S上底面+4S中截面+S下底面),
(S上底面+4S中截面+S下底面),
试判断V估与V的大小关系,并加以证明.
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面.)

(18)如图,在多面体ABCD—A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,
且a>c,b>d,两底面间的距离为h.
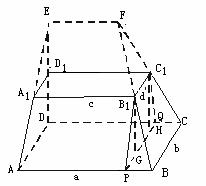
(Ⅰ)求侧面ABB1A1与底面ABCD所成二面角的大小;
(Ⅱ)证明:EF∥面ABCD;
(Ⅲ)在估测该多面体的体积时,经常运用近似公式
V估=S中截面·h来计算.已知它的体积公式是
V=![]() (S上底面+4S中截面+S下底面),试判
(S上底面+4S中截面+S下底面),试判
断V估与V的大小关系,并加以证明.
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面.)
查看习题详情和答案>>如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,上、下底面矩形的长、宽分别为c,d与a,b且a>c,b>d,两底面间的距离为h。
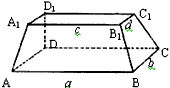
(1)求侧面ABB1A1与底面ABCD所成二面角正切值;
(2)在估测该多面体的体积时,经常运用近似公式V估=S中截面·h来计算,已知它的体积公式是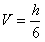 (S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
查看习题详情和答案>>
(2)在估测该多面体的体积时,经常运用近似公式V估=S中截面·h来计算,已知它的体积公式是
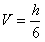 (S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。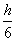 (S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。