题目内容
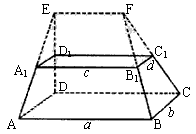
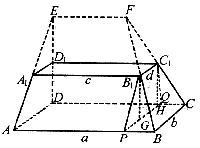
如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b且a>c,b>d,两底面间的距离为h,
(Ⅰ)求侧面ABB1A1与底面ABCD所成二面角的大小;
(Ⅱ)证明:EF∥面ABCD;
(Ⅲ)在估测该多面体的体积时,经常运用近似公式V估=S中截面·h来计算。已知它的体积公式是 V=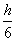 (S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面)
(Ⅰ)求侧面ABB1A1与底面ABCD所成二面角的大小;
(Ⅱ)证明:EF∥面ABCD;
(Ⅲ)在估测该多面体的体积时,经常运用近似公式V估=S中截面·h来计算。已知它的体积公式是 V=
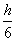 (S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面)
| (Ⅰ)解:过B1C1作底面ABCD的垂直平面, 交底面于PQ,过B1作B1G⊥PQ,垂足为G, ∵平面ABCD∥平面A1B1C1D1,∠A1B1C1=90°, ∴AB⊥PQ,AB⊥B1P, ∴∠B1PG为所求二面角的平面角, 过C1作C1H⊥PQ,垂足为H, 由于相对侧面与底面所成二面角的大小相等, 故四边形B1PQC1为等腰梯形, ∴ 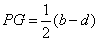 , ,又 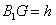 , ,∴ 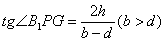 , ,∴ 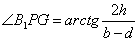 , ,即所求二面角的大小为 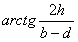 。 。(Ⅱ)证明:∵AB,CD是矩形ABCD的一组对边, 有AB∥CD, 又CD是面ABCD与面CDEF的交线, ∴AB∥面CDEF, ∵EF是面ABFE与面CDEF的交线, ∴AB∥EF, ∵AB是平面ABCD内的一条直线,EF在平面ABCD外, ∴EF∥面ABCD。 (Ⅲ)V估<V; 证明:∵a>c,b>d, ∴ 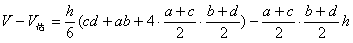  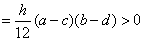 , , ∴V估<V。 |
 |

练习册系列答案
相关题目
 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC, (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC, (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=