摘要:8. 如图.直角坐标系中.一直角三角形...在轴上且关于原点对称.在边上..的周长为12.若一双曲线以.为焦点.且经过.两点. (1) 求双曲线的方程, (2) 若一过点(为非零常数)的直线与双曲线相交于不同于双曲线顶点的两点..且.问在轴上是否存在定点.使?若存在.求出所有这样定点的坐标,若不存在.请说明理由. 解:(1) 设双曲线的方程为. 则. 由.得.即. ∴ 解之得.∴. ∴双曲线的方程为. (2) 设在轴上存在定点.使. 设直线的方程为.. 由.得. 即 ① ∵. . ∴. 即. ② 把①代入②.得 ③ 把代入并整理得 其中且.即且. . 代入③.得 . 化简得 . 当时.上式恒成立. 因此.在轴上存在定点.使.
网址:http://m.1010jiajiao.com/timu3_id_527778[举报]
 (本小题满分12分)
(本小题满分12分)
如图,直角坐标系![]() 中,一直角三角形
中,一直角三角形![]() ,
,![]() ,
,![]() 、
、![]() 在
在![]() 轴上且关于原点
轴上且关于原点![]() 对称,
对称,![]() 在边
在边![]() 上,
上,![]() ,
,![]() 的周长为12.若一双曲线
的周长为12.若一双曲线![]() 以
以![]() 、
、![]() 为焦点,且经过
为焦点,且经过![]() 、
、![]() 两点.(1) 求双曲线
两点.(1) 求双曲线![]() 的方程;
的方程;
(2) 若一过点![]() (
(![]() 为非零常数)的直线
为非零常数)的直线![]() 与双曲线
与双曲线![]() 相交于不同于双曲线顶点的两点
相交于不同于双曲线顶点的两点![]() 、
、![]() ,且
,且![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() ?若存在,求出所有这样定点
?若存在,求出所有这样定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分12分)
如图,在直角坐标系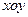 中,已知椭圆
中,已知椭圆 :
: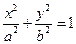
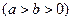 的离心率
的离心率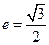 ,左、右两个焦点分别为
,左、右两个焦点分别为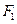 、
、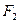 。过右焦点
。过右焦点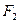 且与
且与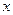 轴垂直的直线与椭圆
轴垂直的直线与椭圆 相交
相交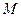 、
、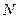 两点,且
两点,且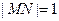 .
.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左顶点为
的左顶点为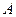 ,下顶点为
,下顶点为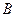 ,动点
,动点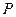 满足
满足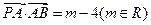 ,试求点
,试求点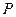 的轨迹方程,使点
的轨迹方程,使点 关于该轨迹的对称点落在椭圆
关于该轨迹的对称点落在椭圆 上.
上.
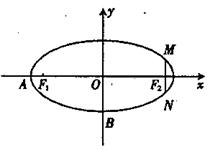
如图,在直角坐标系
 中,已知椭圆
中,已知椭圆 :
: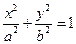
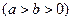 的离心率
的离心率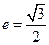 ,左、右两个焦点分别为
,左、右两个焦点分别为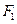 、
、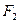 。过右焦点
。过右焦点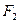 且与
且与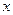 轴垂直的直线与椭圆
轴垂直的直线与椭圆 相交
相交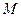 、
、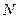 两点,且
两点,且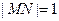 .
.(1)求椭圆
 的方程;
的方程;(2)设椭圆
 的左顶点为
的左顶点为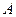 ,下顶点为
,下顶点为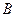 ,动点
,动点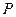 满足
满足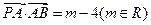 ,试求点
,试求点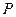 的轨迹方程,使点
的轨迹方程,使点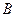 关于该轨迹的对称点落在椭圆
关于该轨迹的对称点落在椭圆 上.
上.
(本小题满分10分)如图,在平面直角坐标系xoy中,A(a,0),B(0,a),C(-4,0),D(0,4)(a>0),设DAOB的外接圆圆心为E。
(1)若圆E与直线CD相切,求实数a的值;
(2)设点P在圆E上,使DPCD的面积等于12的点P有且只有三个,试问这样的圆E是否存在,若存在,求出圆E的标准方程;若不存在,说明理由。

查看习题详情和答案>>

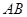 ). 某园林公司承接了该中心花园的施工建设,
). 某园林公司承接了该中心花园的施工建设,