摘要:12. 设函数.其中. (Ⅰ)当时.讨论函数的单调性, (Ⅱ)若函数仅在处有极值.求的取值范围, (Ⅲ)若对于任意的.不等式在上恒成立.求的取值范围. (Ⅰ)解:. 当时. . 令.解得... 当变化时..的变化情况如下表: ↘ 极小值 ↗ 极大值 ↘ 极小值 ↗ 所以在.内是增函数.在.内是减函数. (Ⅱ)解:.显然不是方程的根. 为使仅在处有极值.必须恒成立.即有. 解此不等式.得.这时.是唯一极值. 因此满足条件的的取值范围是. (Ⅲ)解:由条件可知.从而恒成立. 当时.,当时.. 因此函数在上的最大值是与两者中的较大者. 为使对任意的.不等式在上恒成立.当且仅当 即 在上恒成立. 所以.因此满足条件的的取值范围是.
网址:http://m.1010jiajiao.com/timu3_id_527697[举报]
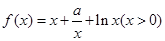 ,其中
,其中 .
.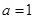 时,求
时,求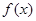 的单调递增区间;
的单调递增区间;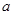 的取值范围,使得对任意的
的取值范围,使得对任意的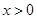 ,都有
,都有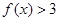 .
.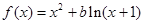 ,其中
,其中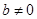 。
。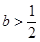 时,判断函数
时,判断函数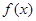 在定义域上的单调性;
在定义域上的单调性;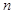 ,不等式
,不等式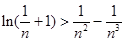 成立。
成立。 ,其中
,其中 。
。 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性; ,不等式
,不等式 成立。
成立。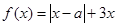 ,其中
,其中 .
. 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为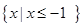 ,求a的值.
,求a的值.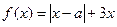 ,其中
,其中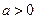 .
.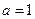 时,求不等式
时,求不等式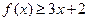 的解集;
的解集;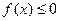 的解集为
的解集为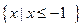 ,求a的值.
,求a的值.