题目内容
(14分)设函数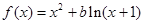 ,其中
,其中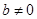 。
。
⑴当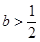 时,判断函数
时,判断函数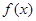 在定义域上的单调性;
在定义域上的单调性;
⑵求函数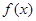 的极值点;
的极值点;
⑶证明对任意的正整数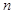 ,不等式
,不等式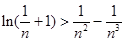 成立。
成立。
【答案】
⑴当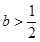 时函数
时函数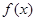 在定义域
在定义域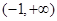 上单调递增
上单调递增
⑵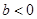 时,
时,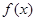 有唯一极小值点
有唯一极小值点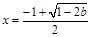 ;
;
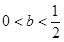 时,
时,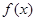 有一个极大值点
有一个极大值点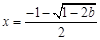 和一个极小值点
和一个极小值点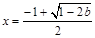 ;
;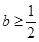 时,
时,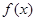 无极值点。
无极值点。
⑶证明见解析
【解析】本试题主要是考查了导数在研究函数中的运用,求解函数的单调性和函数的极值,以及函数与不等式的综合运用。
(1)先求解函数的定义域,然后求解导数,令导数大于零或者小于零得到单调区间。
(2)由⑴得当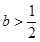 时函数
时函数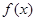 无极值点,接下来对于参数b,进行分类讨论,看导数为零的解,进而确定极值的问题。
无极值点,接下来对于参数b,进行分类讨论,看导数为零的解,进而确定极值的问题。
(3)当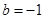 时,函数
时,函数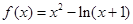 ,令函数
,令函数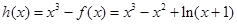 ,
,
则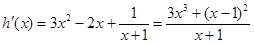 ,当
,当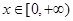 时,
时,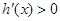
函数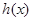 在
在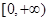 上单调递增,又
上单调递增,又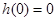 ,
,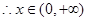 时,恒有
时,恒有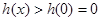
即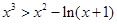 恒成立,从而得到证明。
恒成立,从而得到证明。
解:⑴由题意知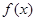 的定义域为
的定义域为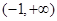 (1分),
(1分),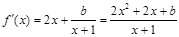
设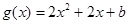 ,其图象的对称轴为
,其图象的对称轴为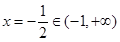 ,
,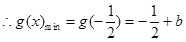
当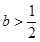 时,
时,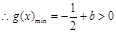 ,即
,即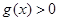 在
在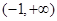 上恒成立,
上恒成立,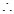 当
当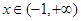 时,
时,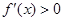
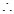 当
当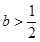 时函数
时函数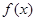 在定义域
在定义域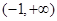 上单调递增。………………………(3分)
上单调递增。………………………(3分)
⑵①由⑴得当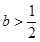 时函数
时函数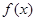 无极值点………………………(4分)
无极值点………………………(4分)
②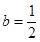 时,
时,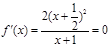 有两个相同的解
有两个相同的解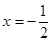
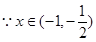 时,
时,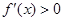 ,
,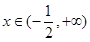 时,
时,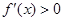
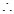
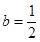 函数
函数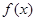 在
在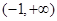 上无极值点………………………(5分)
上无极值点………………………(5分)
③当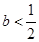 时,
时,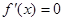 有两个不同解,
有两个不同解,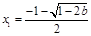 ,
,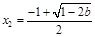
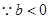 时
时 ,
,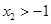 ,即
,即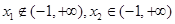
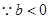 时,
时,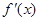 、
、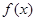 随
随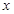 的变化情况如下表:
的变化情况如下表:
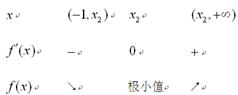
由此表可知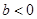 时,
时,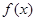 有唯一极小值点
有唯一极小值点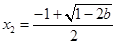 ;………………(7分)
;………………(7分)
当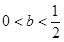 时,
时,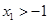 ,
,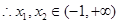 ,此时,
,此时,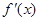 、
、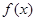 随
随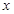 的变化情况如下表:
的变化情况如下表:
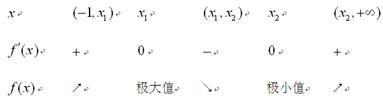
由此表可知: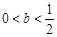 时,
时,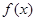 有一个极大值点
有一个极大值点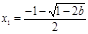 和一个极小值点
和一个极小值点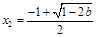 ;……………(9分)
;……………(9分)
综上所述: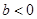 时,
时,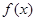 有唯一极小值点
有唯一极小值点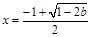 ;
;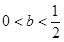 时,
时,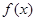 有一个极大值点
有一个极大值点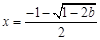 和一个极小值点
和一个极小值点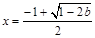 ;
;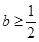 时,
时,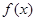 无极值点。(10分)
无极值点。(10分)
⑶当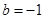 时,函数
时,函数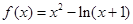 ,令函数
,令函数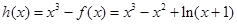 ,
,
则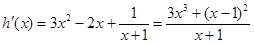 ,当
,当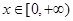 时,
时,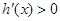
函数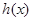 在
在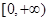 上单调递增,又
上单调递增,又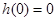 ,
,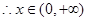 时,恒有
时,恒有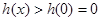
即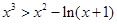 恒成立…………………………(12分)
恒成立…………………………(12分)
故当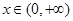 时,有
时,有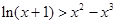 …………………………(13分)
…………………………(13分)
对任意正整数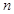 ,取
,取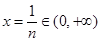 ,则有
,则有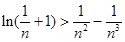 ,故结论成立。……(14分)
,故结论成立。……(14分)

练习册系列答案
相关题目
 ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2. ,其中
,其中
 判断
判断 在
在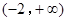 上的单调性.
上的单调性.
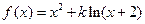 ,其中
,其中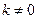
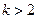 判断
判断 在
在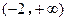 上的单调性.
上的单调性.