题目内容
设双曲线 的两个焦点分别为
的两个焦点分别为 、
、 ,离心率为2.
,离心率为2.
(1)求双曲线的渐近线方程;
(2)过点 能否作出直线
能否作出直线 ,使
,使 与双曲线
与双曲线 交于
交于 、
、 两点,且
两点,且 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.
【解析】(1)根据离心率先求出a2的值,然后令双曲线等于右侧的1为0,解此方程可得双曲线的渐近线方程.
(2)设直线l的方程为 ,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理
,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理 表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
【答案】
∴ 
∴ 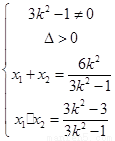
(1)∵
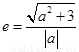 ∴
∴ 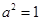 ∴ 双曲线渐近线方程为
∴ 双曲线渐近线方程为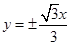
(2)解:假设过点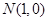 能作出直线
能作出直线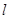 ,使
,使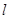 与双曲线
与双曲线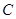 交于
交于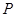 、
、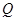 两点,
两点,
且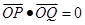 若过点
若过点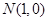 的直线斜率不存在,则不适合题意,舍去.
的直线斜率不存在,则不适合题意,舍去.
设直线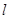 方程为
方程为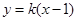
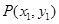
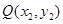
|

①代入②得: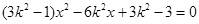
|
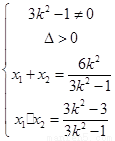
∵ 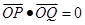 ∴
∴ 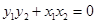 ∴
∴ 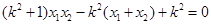
∴ 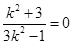 ∴
∴
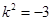 不合题意. ∴
不存在这样的直线.
不合题意. ∴
不存在这样的直线.

练习册系列答案
相关题目
 的两个焦点分别为
的两个焦点分别为 ,离心率为2.
,离心率为2. 的方程;
的方程; 、
、 分别为
分别为 ,求线段
,求线段 的中点
的中点 的轨迹方程,并说明轨迹是什么曲线;
的轨迹方程,并说明轨迹是什么曲线; 分别是双曲线
分别是双曲线 的两个焦点,P是该双曲线上的一点,且
的两个焦点,P是该双曲线上的一点,且 ,则
,则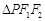 的面积等于
的面积等于 (B)
(B) (C)
(C) (D)
(D)
 分别是双曲线
分别是双曲线 的两个焦点,P是该双曲线上的一点,且
的两个焦点,P是该双曲线上的一点,且 ,则
,则 的面积等于
的面积等于 (B)
(B) (C)
(C) (D)
(D)
 ,且经过点
,且经过点 ,设
,设 是双曲线的两个焦点,点
是双曲线的两个焦点,点 在双曲线上,且
在双曲线上,且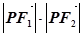 =64.
=64. .
.