摘要:(Ⅰ)当AB⊥x轴时.点A.B关于x轴对称.所以m=0.直线AB的方程为 x=1.从而点A的坐标为(1.)或(1.-). 因为点A在抛物线上.所以.即. 此时C2的焦点坐标为(.0).该焦点不在直线AB上. (Ⅱ)解法一 当C2的焦点在AB时.由(Ⅰ)知直线AB的斜率存在.设直线AB的方程为. 由消去y得. --① 设A.B的坐标分别为(x1,y1), (x2,y2), 则x1,x2是方程①的两根.x1+x2=. 因为AB既是过C1的右焦点的弦.又是过C2的焦点的弦. 所以.且 . 从而. 所以.即. 解得. 因为C2的焦点在直线上.所以. 即. 当时.直线AB的方程为, 当时.直线AB的方程为. 解法二 当C2的焦点在AB时.由(Ⅰ)知直线AB的斜率存在.设直线AB的方程 为. 由消去y得. --① 因为C2的焦点在直线上. 所以.即.代入①有. 即. --② 设A.B的坐标分别为(x1,y1), (x2,y2), 则x1,x2是方程②的两根.x1+x2=. 由消去y得. --③ 由于x1,x2也是方程③的两根.所以x1+x2=. 从而=. 解得. 因为C2的焦点在直线上.所以. 即. 当时.直线AB的方程为, 当时.直线AB的方程为. 解法三 设A.B的坐标分别为(x1,y1), (x2,y2), 因为AB既过C1的右焦点.又是过C2的焦点. 所以. 即. --① 由(Ⅰ)知.于是直线AB的斜率. --② 且直线AB的方程是, 所以. --③ 又因为.所以. --④ 将①.②.③代入④得.即. 当时.直线AB的方程为, 当时.直线AB的方程为.
网址:http://m.1010jiajiao.com/timu3_id_527407[举报]
抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)、A(x1,y1)、B(x2,y2)均在抛物线上.
(1)写出该抛物线的方程及其准线方程.
(2)当PA与PB的斜率存在且倾斜角互补时,求y1+y2的值及直线AB的斜率.
17.如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)、A(x1,y1)、B(x2,y2)均在抛物线上.
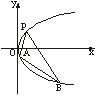
(Ⅰ)写出该抛物线的方程及其准线方程;
(Ⅱ)当PA与PB的斜率存在且倾斜角互补时,求y1+y2的值及直线AB的斜率.
查看习题详情和答案>>
已知△AOB的顶点A在射线l1:y=
x(x>0)上,A,B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足|AM|•|MB|=3.当点A在l1上移动时,记点M的轨迹为W.
(Ⅰ)求轨迹W的方程;
(Ⅱ)设N(2,0),过N的直线l与W相交于P、Q两点.求证:不存在直线l,使得
•
=1.
查看习题详情和答案>>
| 3 |
(Ⅰ)求轨迹W的方程;
(Ⅱ)设N(2,0),过N的直线l与W相交于P、Q两点.求证:不存在直线l,使得
| OP |
| OQ |
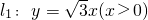 上,A,B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足|AM|•|MB|=3.当点A在l1上移动时,记点M的轨迹为W.
上,A,B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足|AM|•|MB|=3.当点A在l1上移动时,记点M的轨迹为W.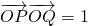 .
.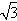 x(x>0),A、B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足
x(x>0),A、B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足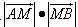 =3,当点A在l1上移动时,记点M的轨迹为W。
=3,当点A在l1上移动时,记点M的轨迹为W。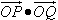 =1?若存在,求出直线l;若不存在,说明理由。
=1?若存在,求出直线l;若不存在,说明理由。