网址:http://m.1010jiajiao.com/timu3_id_527377[举报]
⊙O1和⊙O2的极坐标方程分别为 ,
, .
.
⑴把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
⑵求经过⊙O1,⊙O2交点的直线的直角坐标方程.
【解析】本试题主要是考查了极坐标的返程和直角坐标方程的转化和简单的圆冤啊位置关系的运用
(1)中,借助于公式 ,
, ,将极坐标方程化为普通方程即可。
,将极坐标方程化为普通方程即可。
(2)中,根据上一问中的圆的方程,然后作差得到交线所在的直线的普通方程。
解:以极点为原点,极轴为x轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(I) ,
, ,由
,由 得
得 .所以
.所以 .
.
即 为⊙O1的直角坐标方程.
为⊙O1的直角坐标方程.
同理 为⊙O2的直角坐标方程.
为⊙O2的直角坐标方程.
(II)解法一:由 解得
解得 ,
,
即⊙O1,⊙O2交于点(0,0)和(2,-2).过交点的直线的直角坐标方程为y=-x.
解法二: 由 ,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
查看习题详情和答案>>
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当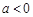 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
查看习题详情和答案>>
设椭圆 (常数
(常数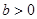 )的左右焦点分别为
)的左右焦点分别为 ,
, 是直线
是直线 上的两个动点,
上的两个动点, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.

【解析】第一问中解:设 ,
, 则
则
由 得
得 由
由 ,得
,得
 ②
②

第二问易求椭圆 的标准方程为:
的标准方程为:
 ,
,
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .
.
解:设 ,
, ……………………1分
……………………1分
则 ,由
,由 得
得 ①……2分
①……2分
(1)由 ,得
,得 ② ……………1分
② ……………1分
 ③ ………………………1分
③ ………………………1分
由①、②、③三式,消去 ,并求得
,并求得 .
………………………3分
.
………………………3分
(2)解法一:易求椭圆 的标准方程为:
的标准方程为: .………………2分
.………………2分
 , ……4分
, ……4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .…2分
.…2分
解法二: ,
………………4分
,
………………4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值
查看习题详情和答案>>