摘要：解 (1)∵点F2关于l的对称点为Q.连接PQ. ∴∠F2PR=∠QPR.|F2R|=|QR|.|PQ|=|PF2| 又因为l为∠F1PF2外角的平分线.故点F1.P.Q在同一直线上.设存在R(x0,y0),Q(x1,y1),F1(-c,0),F2(c,0) |F1Q|=|F2P|+|PQ|=|F1P|+|PF2|=2a,则(x1+c)2+y12=(2a)2 又得x1=2x0-c,y1=2y0 ∴(2x0)2+(2y0)2=(2a)2.∴x02+y02=a2 故R的轨迹方程为 x2+y2=a2(y≠0) (2)如右图.∵S△AOB=|OA|·|OB|·sinAOB=sinAOB 当∠AOB=90°时.S△AOB最大值为a2 此时弦心距|OC|= 在Rt△AOC中.∠AOC=45°.

网址：http://m.1010jiajiao.com/timu3_id_527151[举报]

=1=1（a＞b＞0），点P为其上一点，F₁、F₂为椭圆的焦点，∠F₁PF₂的外角平分线为l，点F₂关于l的对称点为Q，F₂Q交l于点R．
（1）当P点在椭圆上运动时，求R形成的轨迹方程；
（2）设点R形成的曲线为C，直线l：y=k（x+

a）与曲线C相交于A、B两点，当△AOB的面积取得最大值时，求k的值．查看习题详情和答案>>

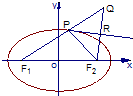
已知椭圆=1(a＞b＞0),点P为其上一点，F₁、F₂为椭圆的焦点，∠F₁PF₂的外角平分线为l，点F₂关于l的对称点为Q，F₂Q交l于点R.

(1)当P点在椭圆上运动时，求R形成的轨迹方程；

(2)设点R形成的曲线为C，直线l: y=k(x+a)与曲线C相交于A、B两点，当△AOB的面积取得最大值时，求k的值.

查看习题详情和答案>>

如下图,已知椭圆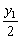

=1(其中a＞b＞0),点P为其上一点,F₁、F₂为焦点, ∠F₁PF₂的外角平分线为l,点F₂关于l的对称点为Q,F₂Q交l于点R.

(1)当P点在椭圆上运动时,求R的轨迹方程;

(2)设点R形成的曲线为C,直线l′:y=k(x+a)与曲线C相交于A、B两点,△AOB的面积为S,求S取得最大值时k的值.

查看习题详情和答案>>

已知椭圆 $数学公式$ + $数学公式$ =1=1（a＞b＞0），点P为其上一点，F₁、F₂为椭圆的焦点，∠F₁PF₂的外角平分线为l，点F₂关于l的对称点为Q，F₂Q交l于点R．
（1）当P点在椭圆上运动时，求R形成的轨迹方程；
（2）设点R形成的曲线为C，直线l：y=k（x+ $数学公式$ a）与曲线C相交于A、B两点，当△AOB的面积取得最大值时，求k的值．

查看习题详情和答案>>

=1=1（a＞b＞0），点P为其上一点，F₁、F₂为椭圆的焦点，∠F₁PF₂的外角平分线为l，点F₂关于l的对称点为Q，F₂Q交l于点R．
（1）当P点在椭圆上运动时，求R形成的轨迹方程；
（2）设点R形成的曲线为C，直线l：y=k（x+

a）与曲线C相交于A、B两点，当△AOB的面积取得最大值时，求k的值．

查看习题详情和答案>>