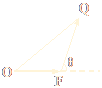题目内容
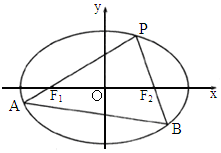
如下图,已知椭圆
(1)当P点在椭圆上运动时,求R的轨迹方程;
(2)设点R形成的曲线为C,直线l′:y=k(x+![]() a)与曲线C相交于A、B两点,△AOB的面积为S,求S取得最大值时k的值.
a)与曲线C相交于A、B两点,△AOB的面积为S,求S取得最大值时k的值.
(1)解法一:连结PQ,
∵F2、Q关于l对称,
∴∠F2PR=∠QPR,F2R=QR,PF2=PQ.
又l为∠F1PF2的外角平分线,故点F1、P、Q在同一直线上.
设R(x0,y0),Q(x1,y1),F1(-c,0), F2(c,0).
|F1Q|=|F1P|+|PQ|=|F1P|+|F2P|=2a.
则(x1+c)2+y12=(2a)2,x0=![]() ,y0=
,y0=![]() .
.
∴x1=2x0-c,y1=2y0.
∴(2x0)2+(2y0)2=(2a)2.
∴x02+y02=a2.
故R的轨迹方程为x2+y2=a2(y≠0).
解法二:同解法一得F1、P、Q共线.
连结OR.
∵|F1O|=|OF2|,|F2R|=|RQ|,
∴|OR|=![]() |F1Q|=
|F1Q|=![]() (|PF1|+|PF2|)=a,
(|PF1|+|PF2|)=a,
即R的轨迹是以O为原点,a为半径的圆.
又P、R不在x轴上,
∴R的轨迹方程为x2+y2=a2(y≠0).
(2)解:∵S△AOB=![]() ·|OA|·|OB|·sin∠AOB=
·|OA|·|OB|·sin∠AOB=![]() sin∠AOB,
sin∠AOB,
当∠AOB=![]() 时,S△AOB的最大值为
时,S△AOB的最大值为![]() a2.
a2.
此时弦心距|OC|=![]() .
.
∵![]() =cos∠AOC=cos
=cos∠AOC=cos![]() =
=![]() ,
,
∴![]() a.
a.
∴k=±![]() .
.
点评:求动点的轨迹方程主要有两种方法:挖掘等式列出方程,或先判断点的轨迹然后求方程.通过本例读者应深刻体会,熟练掌握.

练习册系列答案
相关题目
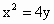 的焦点,离心率等于
的焦点,离心率等于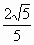 .
.
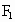 ,
,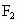 ,
,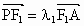 ,
,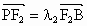 .证明:
.证明: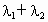 为定值.
为定值.
 的左焦点F,O为坐标原点.
的左焦点F,O为坐标原点.