摘要:4. ⑴ 椭圆的右顶点为(2.0). 设关于直线的对称点为. 则.解得. . .所求椭圆方程为 ⑵ 设A 由 所以---① .---② 因为.即. 所以--③ 由①③得 代入②得..整理得 所以 所以 由于对称性.只需求时.△OAB的面积. 此时.所以
网址:http://m.1010jiajiao.com/timu3_id_527125[举报]
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(I)求椭圆的标准方程;
(II)设G是椭圆上异于A、B的任意一点,GH丄x轴,H为垂足,延长HG到点Q 使得HG=GQ,连接AQ并延长交直线l于点M,点N为MB的中点,判定直线QN与以AB为直径的圆O的位置关系,并证明你的结论.
如图,在平面直角坐标系xOy中,已知椭圆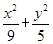 =1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
(1)设动点P满足PF2-PB2=4,求点P的轨迹;
(2)设x1=2,x2=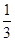 ,求点T的坐标;
,求点T的坐标;
(3)设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).
如图,在平面直角坐标系xOy中,已知椭圆 =1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.

(1)设动点P满足PF2-PB2=4,求点P的轨迹;
(2)设x1=2,x2= ,求点T的坐标;
,求点T的坐标;
(3)设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).
 =1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
(1)设动点P满足PF2-PB2=4,求点P的轨迹;
(2)设x1=2,x2=
 ,求点T的坐标;
,求点T的坐标;(3)设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).