摘要:9.若函数y=log2|ax-1|(a≠0)的图象关于直线x=2成轴对称图形.则a= .
网址:http://m.1010jiajiao.com/timu3_id_526739[举报]
给出下列命题:
①函数y=sin|x|的最小正周期为π;
②若函数f(x)=log2(x2-ax+1)的值域为R,则-2<a<2;
③若函数f(x)对任意x∈R都有f(x)=-f(2-x),且最小正周期为3,则f(x)的图象关于点(-
,0)对称;
④极坐标方程 4sin2θ=3 表示的图形是两条相交直线;
⑤若函数f(x)=(1+x)
(x>0),则存在无数多个正实数M,使得|f(x)|≤M成立;
其中真命题的序号是
查看习题详情和答案>>
①函数y=sin|x|的最小正周期为π;
②若函数f(x)=log2(x2-ax+1)的值域为R,则-2<a<2;
③若函数f(x)对任意x∈R都有f(x)=-f(2-x),且最小正周期为3,则f(x)的图象关于点(-
| 1 |
| 2 |
④极坐标方程 4sin2θ=3 表示的图形是两条相交直线;
⑤若函数f(x)=(1+x)
| 1 |
| x |
其中真命题的序号是
③④⑤
③④⑤
.(写出所有正确命题的序号)
命题
①函数y=f(x)的图象与直线x=a最多有一个交点;
②函数y=-x2+2ax+1在区间(-∞,2]上单调递增,则a∈(-∞,2];
③若 ,当x∈(0,2)时,f(x)=2x,则
,当x∈(0,2)时,f(x)=2x,则 ;
;
④函数y=log2(x2+ax+2)的值域为R,则实数a的取值范围是 ;
;
⑤函数y=f(1+x)与y=f(-x-1)的图象关于y轴对称;
以上命题正确的个数有( )个.
A.2
B.3
C.4
D.5
查看习题详情和答案>>
①函数y=f(x)的图象与直线x=a最多有一个交点;
②函数y=-x2+2ax+1在区间(-∞,2]上单调递增,则a∈(-∞,2];
③若
 ,当x∈(0,2)时,f(x)=2x,则
,当x∈(0,2)时,f(x)=2x,则 ;
;④函数y=log2(x2+ax+2)的值域为R,则实数a的取值范围是
 ;
;⑤函数y=f(1+x)与y=f(-x-1)的图象关于y轴对称;
以上命题正确的个数有( )个.
A.2
B.3
C.4
D.5
查看习题详情和答案>>
命题
①函数y=f(x)的图象与直线x=a最多有一个交点;
②函数y=-x2+2ax+1在区间(-∞,2]上单调递增,则a∈(-∞,2];
③若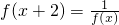 ,当x∈(0,2)时,f(x)=2x,则
,当x∈(0,2)时,f(x)=2x,则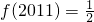 ;
;
④函数y=log2(x2+ax+2)的值域为R,则实数a的取值范围是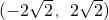 ;
;
⑤函数y=f(1+x)与y=f(-x-1)的图象关于y轴对称;
以上命题正确的个数有______个.
- A.2
- B.3
- C.4
- D.5