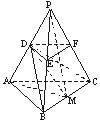摘要：19．如图.在三棱锥P-ABC中,△ABC是边长为2的等边三角形.且∠PCA=∠PCB (1)求证:PCAB, (2)若O为△ABC的中心.G为△PAB的重心.求证:GO∥平面PAC, (3)若. 二面角为锐角.求侧棱PC的取值范围.
网址：http://m.1010jiajiao.com/timu3_id_526507[举报]
如图，在四棱锥P－ABCD中，侧面PAD是正三角形，且垂直于底面ABCD，底面ABC是边长为2的菱形，∠BAD＝60°，M为PC的中点．
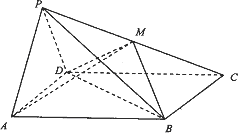
(Ⅰ)求证：PA∥平面BDM；
(Ⅱ)在AD上确定一点
，使得面PB⊥面PBC，并加以证明；
(Ⅲ)求直线AC与平面ADM所成角的正弦值．
如下图，已知三棱锥P－ABC中，E、F分别是以AC、AB的中点，△ABC，△PEF都是正三角形，PF⊥AB．
(1)证明PC⊥平面PAB；
(2)求二面角P－AB－C的平面角的余弦值；
(3)若点P、A、B、C在一个表面积为12π的球面上，求△ABC的边长．
PA，求二面角D－BC－A的大小；(结果用反三角函数值表示)
PA，求二面角D－BC－A的大小；(结果用反三角函数值表示)