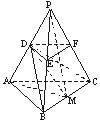题目内容
21.如图，P－ABC是底面边长为1的正三棱锥，D、E、F分别为棱PA、PB、PC上的点，截面DEF∥底面ABC，且棱台DEF－ABC与棱锥P－ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
(1)证明：P－ABC为正四面体；
(2)若PD=
PA，求二面角D－BC－A的大小；(结果用反三角函数值表示)
(3)设棱台DEF—ABC的体积为V，是否存在体积为V且各棱长均相等的平行六面体，使得它与棱台DEF－ABC有相同的棱长和？若存在，请具体构造出这样的一个平行六面体，并给出证明；若不存在，请说明理由.
21. [证明] (1)∵棱锥P－ABC与棱台DEF－ABC的棱长和相等，
∴DE+EF+FD=PD+PE+PF.
又∵截面DEF∥底面ABC，
∴DE=EF=FD=PD=PE=PF，∠DPE=∠EPF=∠FPD=60°,
∴P－ABC为正四面体.
[解] (2)取BC的中点M，连接PM、DM、AM.
∵BC⊥PM，BC⊥AM，∴BC⊥平面PAM，BC⊥DM，
则∠DMA为二面角D－BC－A的平面角.
由(1)知，P－ABC的各棱长均为1，
∴PM=AM=.由D是PA的中点，得sinDMA=
=
,
∴∠DMA=arcsin
.
[解] (3)存在满足条件的直平行六面体.
棱台DEF－ABC的棱长和为定值6，体积为V.
设直平行六面体的棱长均为
，底面相邻两边夹角为α，则该六面体棱长和为12×
=6,体积为
sinα=V.
∵正四面体P－ABC的体积是
，∴0＜V＜
,0＜8V＜1.
可知α=arcsin(8V).
故构造棱长均为
，底面相邻两边夹角为arcsin(8V)的直平行六面体，即满足要求.
练习册系列答案
相关题目
如图三棱柱ABC-A1B1C1中，侧棱BB1与底面成60．角，AQ⊥底面A1B1C1于Q，AP⊥侧面BCC1B1于P，且A1Q⊥B1C1，AB=AC，AQ=3，AP=2则顶点A到棱B1C1的距离是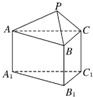
8、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成，现用3种不同颜色对这个几何体的表面染色（底面A1B1C1不涂色），要求相邻的面均不同色，则不同的染色方案共有
如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得．AB=2，BD=1，CE=3，AF=a，O为AB的中点．
PA，求二面角D－BC－A的大小；(结果用反三角函数值表示)