摘要：由三视图知.该多面体是底面为直角三角形的直三棱柱ADE-BCF.且AB＝BC＝BF＝2.DE＝CF＝.∠CBF＝ ①证明:取BF的中点G.连结MG.NG.由M.N分别为AF.BC中点.可得.NG∥CF.MG∥EF --6分 ②取DE中点为H.因为AD＝AE DE 在直三棱柱AED-BCF中 平面ADE⊥平面CDEF 面ADE∩面CDEF＝DE 多面体A-CDEF是以AH为高.以矩形CDEF为底面的棱锥 在△ADE中.AH＝ S矩形CDEF＝DE·EF＝4 --12分
网址：http://m.1010jiajiao.com/timu3_id_524334[举报]
如图，网格纸上小正方形的边长为
，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）
【解析】选
由三视图可知，该几何体是三棱锥，底面是俯视图，高为
，所以几何体的体积为
,选B.
查看习题详情和答案>>
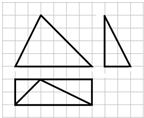（2013•大连一模）如图，网格纸是边长为1的小正方形，在其上用粗线画出了某多面体的三视图，则该多面体的体积为
（2013•大连一模）如图，网格纸是边长为1的小正方形，在其上用粗线画出了某多面体的三视图，则该多面体的体积为（ ）