摘要:19. 在数列中.已知. 且 (1)求证:数列为等比数列, (2)求数列的通项公式, (3)求最大的正整数.使得数列前项和满足.
网址:http://m.1010jiajiao.com/timu3_id_523265[举报]
(本小题满分13分)
已知椭圆的焦点为F1(-4,0),F2(4,0),过点F2且垂直于![]() 轴的直线与椭圆的一个交点为B,且|BF1|+|BF2|=10,设点A,C为椭圆上不同两点,使得|AF2|,|BF2|,|CF2|成等差数列.
轴的直线与椭圆的一个交点为B,且|BF1|+|BF2|=10,设点A,C为椭圆上不同两点,使得|AF2|,|BF2|,|CF2|成等差数列.
(Ⅰ) 求椭圆的标准方程;
(Ⅱ) 求线段AC的中点的横坐标;
(Ⅲ)求线段AC的垂直平分线在y轴上的截距![]() 的取值范围.
的取值范围.
(本小题满分13分)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第![]() 层第
层第![]() 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为![]() .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
(Ⅰ)求![]() 的值,并猜想
的值,并猜想![]() 的表达式.(不必证明)
的表达式.(不必证明)
 (Ⅱ)设小弹子落入第6层第
(Ⅱ)设小弹子落入第6层第![]() 个竖直通道得到分数为
个竖直通道得到分数为![]() ,
,
其中![]() ,试求
,试求![]() 的分布列及数学期望.
的分布列及数学期望.
(本小题满分13分)
已知 分别在射线
分别在射线 (不含端点
(不含端点 )上运动,
)上运动, ,在
,在 中,角
中,角 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 .
.

(Ⅰ)若 、
、 、
、 依次成等差数列,且公差为2.求
依次成等差数列,且公差为2.求 的值;
的值;
(Ⅱ)若 ,
, ,试用
,试用 表示
表示 的周长,并求周长的最大值.
的周长,并求周长的最大值.
查看习题详情和答案>>
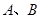 分别在射线
分别在射线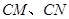 (不含端点
(不含端点 )上运动,
)上运动,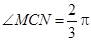 ,在
,在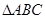 中,角
中,角 、
、 、
、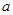 、
、 、
、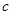 .
.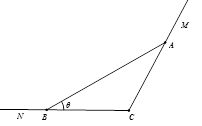
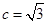 ,
, ,试用
,试用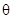 表示
表示 分别在射线
分别在射线 (不含端点
(不含端点 )上运动,
)上运动, ,在
,在 中,角
中,角 、
、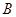 、
、 、
、 、
、 .
.
 ,
, ,试用
,试用 表示
表示