摘要：重视数学思想方法的复习根据本章上述的命题趋向我们迎考复习时应加强数学思想方法的复习.在复习不等式的解法时.加强等价转化思想的训练与复习.解不等式的过程是一个等价转化的过程.通过等价转化可简化不等式(组).以快速.准确求解.加强分类讨论思想的复习.在解不等式或证不等式的过程中.如含参数等问题.一般要对参数进行分类讨论.复习时.学生要学会分析引起分类讨论的原因.合理的分类.做到不重不漏.加强函数与方程思想在不等式中的应用训练.不等式.函数.方程三者密不可分.相互联系.互相转化.如求参数的取值范围问题.函数与方程思想是解决这类问题的重要方法.在不等式的证明中.加强化归思想的复习.证不等式的过程是一个把已知条件向要证结论的一个转化过程.既可考查学生的基础知识.又可考查学生分析问题和解决问题的能力.正因为证不等式是高考考查学生代数推理能力的重要素材.复习时应引起我们的足够重视.利用函数f的单调性解决有关最值问题是近几年高考中的热点.应加强这方面的训练和指导.
网址：http://m.1010jiajiao.com/timu3_id_523172[举报]
（2013•福建）当x∈R，|x|＜1时，有如下表达式：1+x+x2+…+xn+…=
两边同时积分得：
1dx+
xdx+
x2dx+…
xndx+…=
dx
从而得到如下等式：1×
+
×(
)2+
×(
)3+…+
×(
)n+1+…=ln2．
请根据以上材料所蕴含的数学思想方法，计算：
×
+
×(
)2+
×(
)3+…+
×(
)n+1=
[(
)n+1-1]
[(
)n+1-1]．
查看习题详情和答案>>
| 1 |
| 1-x |
两边同时积分得：
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| 1 |
| 1-x |
从而得到如下等式：1×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
请根据以上材料所蕴含的数学思想方法，计算：
| C | 0 n |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 2 |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 2 |
| 1 |
| n+1 |
| C | n n |
| 1 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
的定义域为
且
，对任意
都有
满足
N
.证明函数
的通项公式;令
N
时,
.
时，有如下表达式:
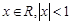时，有如下表达式： 
两边同时积分得：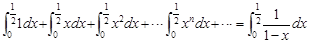
（a>b>0）,点
在椭圆上。