摘要：加大推理.论证能力的考查力度.充分体现由知识立意向能力立意转变的命题方向.由于代数推理没有几何图形作依托.因而更能检测出学生抽象思维能力的层次.这类代数推理问题常以高中代数的主体内容--函数.方程.不等式.数列及其交叉综合部分为知识背景.并与高等数学知识及思想方法相衔接.立意新颖.抽象程度高.有利于高考选拔功能的充分发挥.对不等式的考查更能体现出高观点.低设问.深入浅出的特点.考查容量之大.功能之多.能力要求之高.一直是高考的热点.
网址：http://m.1010jiajiao.com/timu3_id_523166[举报]
（本小题满分13分）
已知中心在坐标原点O的椭圆C经过点A（2，3），且点F（2，0）为其右焦点。
（1）求椭圆C的方程；
（2）是否存在平行于OA的直线
，使得直线与椭圆C有公共点，且直线OA与的距离等于4？若存在，求出直线的方程；若不存在，请说明理由。
【命题意图】本小题主要考查直线、椭圆等基础知识，考查运算求解能力、推理论证能力，考查函数与方程思想、数形结合思想、化归与转化思想。
查看习题详情和答案>>（本小题满分13分）
已知中心在坐标原点O的椭圆C经过点A（2，3），且点F（2，0）为其右焦点。
（1）求椭圆C的方程；
（2）是否存在平行于OA的直线
，使得直线与椭圆C有公共点，且直线OA与的距离等于4？若存在，求出直线的方程；若不存在，请说明理由。
【命题意图】本小题主要考查直线、椭圆等基础知识，考查运算求解能力、推理论证能力，考查函数与方程思想、数形结合思想、化归与转化思想。
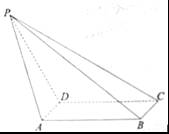
查看习题详情和答案>>如图，在四棱锥P-ABCD中，底面ABCD是矩形，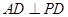
，BC=1，
，PD=CD=2.
（I）求异面直线PA与BC所成角的正切值；
（II）证明平面PDC⊥平面ABCD；
（III）求直线PB与平面ABCD所成角的正弦值。
【考点定位】本小题主要考查异面直线所成的角、平面与平面垂直、直线与平面所成的角等基础知识.，考查空间想象能力、运算求解能力和推理论证能力.
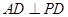，BC=1，，PD=CD=2.（I）求异面直线PA与BC所成角的正切值；
（II）证明平面PDC⊥平面ABCD；
（III）求直线PB与平面ABCD所成角的正弦值。
【考点定位】本小题主要考查异面直线所成的角、平面与平面垂直、直线与平面所成的角等基础知识.，考查空间想象能力、运算求解能力和推理论证能力.
，BC=1，
，PD=CD=2.
是等差数列，其前n项和为
， 
是等比数列，且
求证：
,
。