摘要:6.(北师大版第64页A组第9题)图像变换 变式1: 解:函数可转化为二次函数.作出函数图像.由图像可得单调区间. 当时.. 当时.. 作出函数图像.由图像可得单调区间. 在和上.函数是增函数,在和上.函数是减函数. 变式2: 解:若则.显然不是偶函数.所以①是不正确的, 若则.满足.但的图像不关于直线x=1对称.所以②是不正确的, 若.则.图像是开口向上的抛物线.其对称轴是.∴在区间[a.+∞上是增函数.即③是正确的, 显然函数没有最大值.所以④是不正确的. 变式3: 解:. (1)当c=0时..满足.是奇函数.所以①是正确的, (2)当b=0.c>0时.. 方程即 或 . 显然方程无解,方程的唯一解是 .所以② 是正确的, (3)设是函数图像上的任一点.应有. 而该点关于(0.c)对称的点是.代入检验即.也即.所以也是函数图像上的点.所以③是正确的, (4)若.则.显然方程有三个根.所以④ 是不正确的.
网址:http://m.1010jiajiao.com/timu3_id_522030[举报]
已知函数f(x)=Asin(ωx+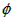 )+b
)+b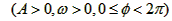 在同一周期内有最高点(
在同一周期内有最高点(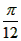 ,1)和最低点(
,1)和最低点(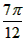 ,-3)
,-3)
(1)求f(x)的解析式及f(x)=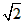 -1的解集;
-1的解集;
(2)将f(x)的图像向右平移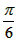 个单位,再将横坐标扩大为原来的2倍(纵坐标不变)后得到g(x)的函数图像,写出g(x)的解析式;
个单位,再将横坐标扩大为原来的2倍(纵坐标不变)后得到g(x)的函数图像,写出g(x)的解析式;
查看习题详情和答案>>
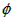 )+b
)+b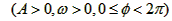 在同一周期内有最高点(
在同一周期内有最高点(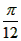 ,1)和最低点(
,1)和最低点(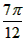 ,-3)
,-3)(1)求f(x)的解析式及f(x)=
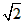 -1的解集;
-1的解集;(2)将f(x)的图像向右平移
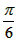 个单位,再将横坐标扩大为原来的2倍(纵坐标不变)后得到g(x)的函数图像,写出g(x)的解析式;
个单位,再将横坐标扩大为原来的2倍(纵坐标不变)后得到g(x)的函数图像,写出g(x)的解析式;
给出下列4个命题:
①保持函数y=sin(2x+
)图象的纵坐标不变,将横坐标扩大为原来的2倍,得到的图象的解析式为y=sin(x+
).
②在区间[0,
)上,x0是y=tanx的图象与y=cosx的图象的交点的横坐标,则
<x0<
.
③在平面直角坐标系中,取与x轴、y轴正方向相同的两个单位向量
,
作为基底,则四个向量
+2
,
+
,
-
,2
-
的坐标表示的点共圆.
④方程cos3x-sin3x=1的解集为{x|x=2kπ-
,k∈Z}.
其中正确的命题的序号为 .
查看习题详情和答案>>
①保持函数y=sin(2x+
| π |
| 3 |
| π |
| 6 |
②在区间[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 4 |
③在平面直角坐标系中,取与x轴、y轴正方向相同的两个单位向量
| i |
| j |
| i |
| j |
| 2 |
| i |
| 3 |
| j |
| 3 |
| i |
| 2 |
| j |
| i |
| j |
④方程cos3x-sin3x=1的解集为{x|x=2kπ-
| π |
| 2 |
其中正确的命题的序号为
将函数y=sinx的图象C按顺序作以下两种变换:(1)向左平移
个单位长度;(2)横坐标伸长到原来的2倍,纵坐标不变.所得到的曲线C/对应的函数解析式是( )
| π |
| 3 |
A、y=sin(2x-
| ||||
B、y=sin(
| ||||
C、y=sin(2x+
| ||||
D、y=sin(
|
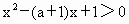 .
.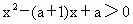
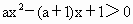 ,(a≠0)
,(a≠0)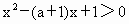 .
.
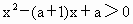
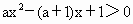 ,(a≠0)
,(a≠0)