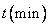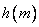摘要：3．函数方程思想的几种重要形式 (1)函数和方程是密切相关的.对于函数y＝f(x).当y＝0时.就转化为方程f(x)＝0.也可以把函数式y＝f＝0. (2)函数与不等式也可以相互转化.对于函数y＝f(x).当y＞0时.就转化为不等式f(x)＞0.借助于函数图像与性质解决有关问题.而研究函数的性质.也离不开解不等式, (3)数列的通项或前n项和是自变量为正整数的函数.用函数的观点处理数列问题十分重要, ^n (n∈N*)与二项式定理是密切相关的.利用这个函数用赋值法和比较系数法可以解决很多二项式定理的问题, (5)解析几何中的许多问题.例如直线和二次曲线的位置关系问题.需要通过解二元方程组才能解决.涉及到二次方程与二次函数的有关理论, (6)立体几何中有关线段.角.面积.体积的计算.经常需要运用布列方程或建立函数表达式的方法加以解决. 2 经典例题剖析 (根据近几年高考命题知识点及热点做相应的试题剖析.要求例题不得少于8个)
网址：http://m.1010jiajiao.com/timu3_id_522002[举报]
（2008•普陀区二模）经济学中有一个用来权衡企业生产能力（简称“产能”）的模型，称为“产能边界”．它表示一个企业在产能最大化的条件下，在一定时期内所能生产的几种产品产量的各种可能的组合．例如，某企业在产能最大化条件下，一定时期内能生产A产品x台和B产品y台，则它们之间形成的函数y=f（x）就是该企业的“产能边界函数”．现假设该企业的“产能边界函数”为y=15| 1600-2x |
（1）试分析该企业的产能边界，分别选用①、②、③中的一个序号填写下表：
| 点Pi（x，y）对应的产量组合 | 实际意义 |
| P1（350，450） | ③ |
| P2（200，300） | |
| P3（500，400） | |
| P4（408，420） |
②这是一种生产目标脱离产能实际的产量组合；
③这是一种使产能最大化的产量组合．
（2）假设A产品每台利润为a（a＞0）元，B产品每台利润为A产品每台利润的2倍．在该企业的产能边界条件下，试为该企业决策，应生产A产品和B产品各多少台才能使企业从中获得最大利润？
某工厂6年来生产某种产品的总产量C(即前t年产量之和)与时间t(年)的函数关系如图所示,则关于下面的几种说法中正确的是_________.
①前三年中,年产量增长的速度越来越快
②前三年中,年产量增长的速度越来越慢
③后三年中,这种产品的年产量保持不变
④第三年中,这种产品停止生产
查看习题详情和答案>>
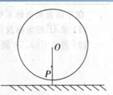在生活中有很多现象具有周期性，大家学过的三角函数就是描述周期现象的一种重要的数学模型，假设游乐场中的摩天轮匀速旋转，其中心
距离地面30.5m，半径30m。若从最低点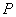
处登上摩天轮，从你登上摩天轮开始计时，那么你与地面的距离
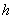将随时间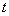
变化，并且经过6min到达最高点，请完成下列问题：
（1）填写表格：
|
|
0 |
3 |
6 |
9 |
12 |
|
|
|
|
|
|
|
（2）求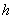与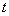之间的函数关系式
；
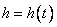（3）当你在摩天轮上转第一圈，并且距离地面15.5m时，所用时间是多少？当你在摩天轮上转第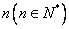
圈，并且距离地面15.5m，所用时间是多少？
查看习题详情和答案>>
经济学中有一个用来权衡企业生产能力（简称“产能”）的模型，称为“产能边界”．它表示一个企业在产能最大化的条件下，在一定时期内所能生产的几种产品产量的各种可能的组合．例如，某企业在产能最大化条件下，一定时期内能生产A产品x台和B产品y台，则它们之间形成的函数y=f（x）就是该企业的“产能边界函数”．现假设该企业的“产能边界函数”为
（如图）．
（1）试分析该企业的产能边界，分别选用①、②、③中的一个序号填写下表：
①这是一种产能未能充分利用的产量组合；
②这是一种生产目标脱离产能实际的产量组合；
③这是一种使产能最大化的产量组合．
（2）假设A产品每台利润为a（a＞0）元，B产品每台利润为A产品每台利润的2倍．在该企业的产能边界条件下，试为该企业决策，应生产A产品和B产品各多少台才能使企业从中获得最大利润？
查看习题详情和答案>>
（如图）．（1）试分析该企业的产能边界，分别选用①、②、③中的一个序号填写下表：
| 点Pi（x，y）对应的产量组合 | 实际意义 |
| P1（350，450） | ③ |
| P2（200，300） | |
| P3（500，400） | |
| P4（408，420） |
②这是一种生产目标脱离产能实际的产量组合；
③这是一种使产能最大化的产量组合．
（2）假设A产品每台利润为a（a＞0）元，B产品每台利润为A产品每台利润的2倍．在该企业的产能边界条件下，试为该企业决策，应生产A产品和B产品各多少台才能使企业从中获得最大利润？
查看习题详情和答案>>
经济学中有一个用来权衡企业生产能力（简称“产能”）的模型，称为“产能边界”．它表示一个企业在产能最大化的条件下，在一定时期内所能生产的几种产品产量的各种可能的组合．例如，某企业在产能最大化条件下，一定时期内能生产A产品x台和B产品y台，则它们之间形成的函数y=f（x）就是该企业的“产能边界函数”．现假设该企业的“产能边界函数”为
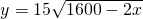（如图）．
（1）试分析该企业的产能边界，分别选用①、②、③中的一个序号填写下表：
| 点Pi（x，y）对应的产量组合 | 实际意义 |
| P1（350，450） | ③ |
| P2（200，300） | |
| P3（500，400） | |
| P4（408，420） |
②这是一种生产目标脱离产能实际的产量组合；
③这是一种使产能最大化的产量组合．
（2）假设A产品每台利润为a（a＞0）元，B产品每台利润为A产品每台利润的2倍．在该企业的产能边界条件下，试为该企业决策，应生产A产品和B产品各多少台才能使企业从中获得最大利润？ 查看习题详情和答案>>