摘要:如图.在△ABC中.角A.B.C的对边分别为..c, 且8=7..AB边上的高CM长为. (Ⅰ)求的值, (Ⅱ)求△ABC的面积 设数列的前项和为.且,数列为等差数列.且.. (Ⅰ)求数列的通项公式, (Ⅱ)若.为数列的前项和. 求证:. 有10张形状.大小相同的卡片.其中2张上写着数字.另外5张上写着数字1.余下3张上写着数字2.从中随机地取出1张.记下它的数字后放回原处.当这种手续重复进行2次时.为所记下的两个数之和. (Ⅰ)求=2时的概率, (Ⅱ)求的数学期望, 如图.平面⊥平面.为正方形.. 且分别是线段的中点. (Ⅰ)求证://平面, (Ⅱ)求异面直线与所成的角, (Ⅲ)在线段上是否存在一点.使得点到平面的距离为; 若存在.求出的值,若不存在.请说明理由. 已知椭圆的离心率为.直线:与以原点为圆心.以椭圆的短半轴长为半径的圆相切. (Ⅰ)求椭圆的方程, (Ⅱ)设椭圆的左焦点为.右焦点.直线过点且垂直于椭圆的长轴.动直线垂直于点.线段垂直平分线交于点.求点的轨迹的方程, 中的与轴交于点.不同的两点在上.且满足求的取值范围. 已知.b为函数的极值点 (Ⅰ)求证:; (Ⅱ)判断函数上的单调性.并证明你的结论, (Ⅲ)若曲线处的切线斜率为-4.且方程有两个不等的实根.求实数的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_521449[举报]
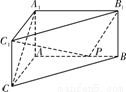
(本小题满分12分)如图,在直三棱柱ABC―A1B1C1中,∠ACB = 90°. AC = BC = a,
D、E分别为棱AB、BC的中点, M为棱AA1上的点,二面角M―DE―A为30°.
(1)求MA的长;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)求点C到平面MDE的距离。

( (本小题满分12分) 如图,在直三棱柱ABC—A1B1C1中, .
.
(Ⅰ)若D为AA1中点,求证:平面B1CD 平面B1C1D;
平面B1C1D;
(Ⅱ)若二面角B1—DC—C1的大小为60°,求AD的长.

 .
. 平面B1C1D;
平面B1C1D;