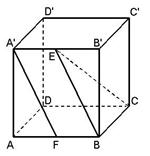
摘要:19. 如图.在棱长为2的正方体ABCD -A1B1C1D1中.E.F分别为AA1.和CC1的中点. (I)求证:EF∥平面ACD., (Ⅱ)求异面直线EF与AB所成的角, (Ⅲ)在棱BB1上是否存在一点P.使得二面角P-AC-B的大小为30°?若存在.求出BP的长,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_520986[举报]
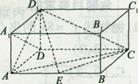
(本小题满分12分)如图,在直三棱柱ABC―A1B1C1中,∠ACB = 90°. AC = BC = a,
D、E分别为棱AB、BC的中点, M为棱AA1上的点,二面角M―DE―A为30°.
(1)求MA的长;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)求点C到平面MDE的距离。

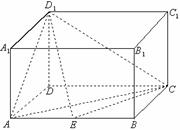
(本小题满分12分)如图,在长方体ABCD-A1B1C1D1中,AD=AAl=1,AB=2,点E在棱AB上移动.
(I)证明:D1E上AlD;
(Ⅱ)当E为AB的中点时,求点E到面ACD1的距离;
(Ⅲ)在(II)的条件下,求D1E与平面AD1C所成角的正弦值.

查看习题详情和答案>>