摘要:27.已知AB是抛物线的任一弦.F为抛物线的焦点.l为准线.m是过点A且以向量为方向向量的直线. (1)若过点A的抛物线的切线与y轴相交于点C.求证:|AF|=|CF|, (2)若异于原点).直线OB与m相交于点P.求点P的轨迹方程, (3)若AB过焦点F.分别过A.B的抛物线两切线相交于点T.求证:且T在直线l上. 解:(1)设A(.因为导数. 则直线AC的方程: 由抛物线定义知.|AF|=+.又|CF|=-(-)=+.故|AF|=|CF|. (2)设 由 得. ① 直线OB方程: ② 直线m的方程:. ③ 由①②③得y=-p.故点P的轨迹方程为y=-p(x≠0). (3)设则 因为AB是焦点弦.设AB的方程为: 得 由(1)知直线AT方程: 同理直线BT方程: 所以直线AB方程:. 又因为AB过焦点..故T在准线上.
网址:http://m.1010jiajiao.com/timu3_id_520904[举报]
已知直线AB是抛物线x2=2py的任意一条弦,F是其焦点
①若
•
+p2=0(A,B异于原点)过A作x轴垂线l,直线OB交l于P,求点P轨迹方程;
②若AB过焦点F,抛物线以A,B为切点的两切线交于点T,求证AT⊥BT,并指明点T在定直线上运动.
查看习题详情和答案>>
①若
| OA |
| OB |
②若AB过焦点F,抛物线以A,B为切点的两切线交于点T,求证AT⊥BT,并指明点T在定直线上运动.
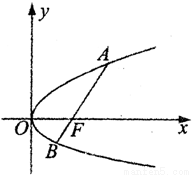
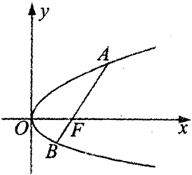 已知抛物线y2=2px(p>0)过焦点F的任一条弦AB,设A(x1,y1),B(x2,y2)且y1>0,y2<0
已知抛物线y2=2px(p>0)过焦点F的任一条弦AB,设A(x1,y1),B(x2,y2)且y1>0,y2<0
(1)若y1y2=-4,求抛物线方程;
(2)是否存在常数λ,使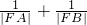 =λ,若存在,求出λ的值,并给予证明,若不存在,请说明理由;
=λ,若存在,求出λ的值,并给予证明,若不存在,请说明理由;
(3)在抛物线对称轴(ox的正方向)上是否存在一定点M,经过点M的任意一条弦AB,使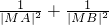 为定值,若存在,则求出定点M的坐标和定值,若不存在,请说明理由.
为定值,若存在,则求出定点M的坐标和定值,若不存在,请说明理由.
查看习题详情和答案>>
已知中心的坐标原点,以坐标轴为对称轴的双曲线C过点Q(2,
),且点Q在x轴上的射影恰为该双曲线的一个焦点F1
(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆
+
=1的一个焦点F作与x轴不垂直的任意直线l”交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
为定值,且定值是
”.命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F、M两点间距离的比值.试类比上述命题,写出一个关于抛物线C的类似的正确命题,并加以证明
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明).
查看习题详情和答案>>
| ||
| 3 |
(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆
| x2 |
| 25 |
| y2 |
| 16 |
| |AB| |
| |FM| |
| 10 |
| 3 |
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明).
已知中心在坐标原点,以坐标轴为对称轴的双曲线C过点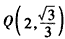 ,且点Q在x轴上的射影恰为该双曲线的一个焦点F,
,且点Q在x轴上的射影恰为该双曲线的一个焦点F,
(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆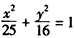 的一个焦点F作与x轴不垂直的任意直线l交椭圆于A.B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F作与x轴不垂直的任意直线l交椭圆于A.B两点,线段AB的垂直平分线交x轴于点M,则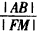 为定值,且定值是
为定值,且定值是 ”。命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F,M两点间的距离的比值.
”。命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F,M两点间的距离的比值.
试类比上述命题,写出一个关于双曲线C的类似的正确命题,并加以证明;
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明)。
查看习题详情和答案>>
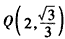 ,且点Q在x轴上的射影恰为该双曲线的一个焦点F,
,且点Q在x轴上的射影恰为该双曲线的一个焦点F,(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆
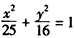 的一个焦点F作与x轴不垂直的任意直线l交椭圆于A.B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F作与x轴不垂直的任意直线l交椭圆于A.B两点,线段AB的垂直平分线交x轴于点M,则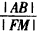 为定值,且定值是
为定值,且定值是 ”。命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F,M两点间的距离的比值.
”。命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F,M两点间的距离的比值.试类比上述命题,写出一个关于双曲线C的类似的正确命题,并加以证明;
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明)。
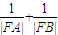 =λ,若存在,求出λ的值,并给予证明,若不存在,请说明理由;
=λ,若存在,求出λ的值,并给予证明,若不存在,请说明理由;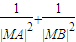 为定值,若存在,则求出定点M的坐标和定值,若不存在,请说明理由.
为定值,若存在,则求出定点M的坐标和定值,若不存在,请说明理由.