题目内容
已知中心在坐标原点,以坐标轴为对称轴的双曲线C过点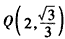 ,且点Q在x轴上的射影恰为该双曲线的一个焦点F,
,且点Q在x轴上的射影恰为该双曲线的一个焦点F,
(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆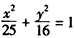 的一个焦点F作与x轴不垂直的任意直线l交椭圆于A.B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F作与x轴不垂直的任意直线l交椭圆于A.B两点,线段AB的垂直平分线交x轴于点M,则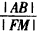 为定值,且定值是
为定值,且定值是 ”。命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F,M两点间的距离的比值.
”。命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F,M两点间的距离的比值.
试类比上述命题,写出一个关于双曲线C的类似的正确命题,并加以证明;
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明)。
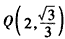 ,且点Q在x轴上的射影恰为该双曲线的一个焦点F,
,且点Q在x轴上的射影恰为该双曲线的一个焦点F,(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆
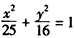 的一个焦点F作与x轴不垂直的任意直线l交椭圆于A.B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F作与x轴不垂直的任意直线l交椭圆于A.B两点,线段AB的垂直平分线交x轴于点M,则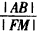 为定值,且定值是
为定值,且定值是 ”。命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F,M两点间的距离的比值.
”。命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F,M两点间的距离的比值.试类比上述命题,写出一个关于双曲线C的类似的正确命题,并加以证明;
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明)。
解:(Ⅰ)依题意,可设双曲线C的方程为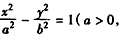
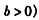 ,
,
由已知得C的一个焦点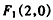 ,
,
所以C的另一个焦点为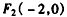 ,
,
由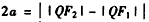
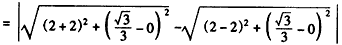
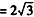 ,
,
得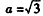 ,
,
又a=2,
所以,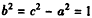 ,
,
所以,双曲线C的方程为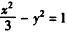 。
。
(Ⅱ)关于双曲线C的类似命题为:过双曲线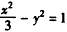 的焦点F1(2,0)作与x轴不垂直的任意直线l交双曲线于A,B两点,线段AB的垂直平分线交x轴于点M,则
的焦点F1(2,0)作与x轴不垂直的任意直线l交双曲线于A,B两点,线段AB的垂直平分线交x轴于点M,则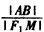 为定值,且定值是
为定值,且定值是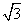 。
。
证明如下:由于l与x轴不垂直,可设直线l的方程为:y=k(x-2),
①当k=0时,l与x轴重合,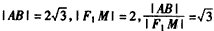 ,命题正确;
,命题正确;
②当k≠0时,由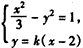 得
得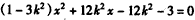 ,
,
依题意l与C有两个交点A,B,所以,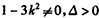 ,
,
设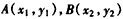 ,
,
则 ,
,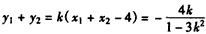 ,
,
所以线段AB的中点P的坐标为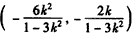 ,
,
AB的垂直平分线MP的方程为: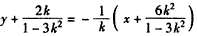 ,
,
令y=0,解得: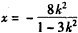 ,
,
即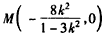 ,所以,
,所以,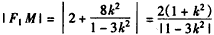 ,
,
又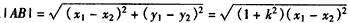
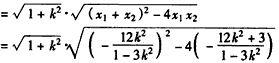
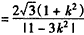 ,
,
所以,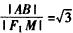 。
。
(Ⅲ)过圆锥曲线E的焦点F作与焦点所在的对称轴不垂直的任意直线l交E于A,B两点,线段AB的垂直平分线交焦点所在的对称轴于点M,则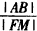 为定值,定值是
为定值,定值是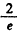 (其中e为圆锥曲线E的离心率)。
(其中e为圆锥曲线E的离心率)。
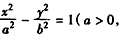
 ,
,由已知得C的一个焦点
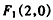 ,
,所以C的另一个焦点为
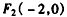 ,
,由
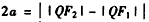
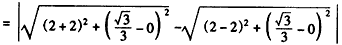
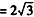 ,
,得
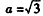 ,
,又a=2,
所以,
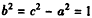 ,
,所以,双曲线C的方程为
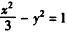 。
。(Ⅱ)关于双曲线C的类似命题为:过双曲线
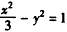 的焦点F1(2,0)作与x轴不垂直的任意直线l交双曲线于A,B两点,线段AB的垂直平分线交x轴于点M,则
的焦点F1(2,0)作与x轴不垂直的任意直线l交双曲线于A,B两点,线段AB的垂直平分线交x轴于点M,则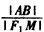 为定值,且定值是
为定值,且定值是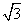 。
。证明如下:由于l与x轴不垂直,可设直线l的方程为:y=k(x-2),
①当k=0时,l与x轴重合,
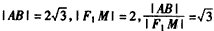 ,命题正确;
,命题正确; ②当k≠0时,由
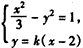 得
得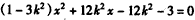 ,
,依题意l与C有两个交点A,B,所以,
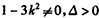 ,
,设
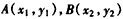 ,
,则
 ,
,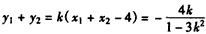 ,
,所以线段AB的中点P的坐标为
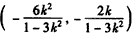 ,
,AB的垂直平分线MP的方程为:
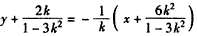 ,
,令y=0,解得:
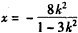 ,
,即
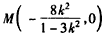 ,所以,
,所以,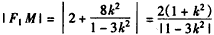 ,
,又
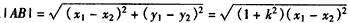
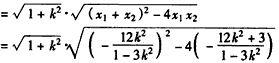
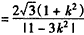 ,
,所以,
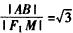 。
。(Ⅲ)过圆锥曲线E的焦点F作与焦点所在的对称轴不垂直的任意直线l交E于A,B两点,线段AB的垂直平分线交焦点所在的对称轴于点M,则
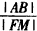 为定值,定值是
为定值,定值是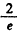 (其中e为圆锥曲线E的离心率)。
(其中e为圆锥曲线E的离心率)。 
练习册系列答案
相关题目
 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率