题目内容
已知中心的坐标原点,以坐标轴为对称轴的双曲线C过点Q(2,
),且点Q在x轴上的射影恰为该双曲线的一个焦点F1
(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆
+
=1的一个焦点F作与x轴不垂直的任意直线l”交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
为定值,且定值是
”.命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F、M两点间距离的比值.试类比上述命题,写出一个关于抛物线C的类似的正确命题,并加以证明
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明).
| ||
| 3 |
(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆
| x2 |
| 25 |
| y2 |
| 16 |
| |AB| |
| |FM| |
| 10 |
| 3 |
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明).
(I)由题意可设双曲线C的方程为
-
=1(a>0,b>0)
∵点Q(2,
),且点Q在x轴上的射影恰为该双曲线的一个焦点F1
∴双曲线C的一个焦点为F1(2,0)可得C的另一个焦点为F2(-2,0)(1分)
由2a=||QF1|-|QF2||=|
-
|=2
(3分)
∴a=
,又c=2,所以b2=c2-a2=1(4分)
双曲线的方程为
-y2=1
(II)关于抛物线C的类似命题为:过抛物线y2=4x的焦点F1(1,0)作与x轴不垂直的任意直线L交抛物线于点A,B两点,线段AB的垂直平分线交x轴于点M,则
为定值,定值是2(6分)
证明如下:由于直线与x轴不垂直,可设直线L的方程为y=k(x-1)(k≠0)
联立方程
可得k2x2-2(k2+2)x+k2=0
由题意L与C有两个交点A,B,则k2≠0,△>0
设A(x1,y1),B(x2,y2)
则x1+x2=
,x1x2=1,y1+y2=k(x1+x2-2)=
∴线段AB的中点P的坐标(
,
)(8分)
AB的垂直平分线MP的方程为y-
=-
(x-
)
令y=0可得,x=3+
即M(3+
,0),F1(1,0)
∴|MF1|=2+
(9分)
∵|AB|=
=
=
=
+4
∴
=2(10分)
(III)过圆锥曲线E的焦点F作与焦点所在的对称轴不垂直的任意直线L交于A,B两点,线段AB的垂直平分线交焦点所在的对称轴于点M,则
为定值,定值是
(其中e 是圆锥曲线E的离心率)(13分)
(法二)由题意可设双曲线C的方程为
-
=1(a>0,b>0)(1分)
由已知可得
(3分)
解可得,
∴双曲线的方程为
-y2=1(4分)
(II ),(III)同法一
| x2 |
| a2 |
| y2 |
| b2 |
∵点Q(2,
| ||
| 3 |
∴双曲线C的一个焦点为F1(2,0)可得C的另一个焦点为F2(-2,0)(1分)
由2a=||QF1|-|QF2||=|
(2+2)2+(
|
(2-2)2+(
|
| 3 |
∴a=
| 3 |
双曲线的方程为
| x2 |
| 3 |
(II)关于抛物线C的类似命题为:过抛物线y2=4x的焦点F1(1,0)作与x轴不垂直的任意直线L交抛物线于点A,B两点,线段AB的垂直平分线交x轴于点M,则
| |AB| |
| |MF1| |
证明如下:由于直线与x轴不垂直,可设直线L的方程为y=k(x-1)(k≠0)
联立方程
|
由题意L与C有两个交点A,B,则k2≠0,△>0
设A(x1,y1),B(x2,y2)
则x1+x2=
| 2(k2+2) |
| k2 |
| 4 |
| k |
∴线段AB的中点P的坐标(
| k2+2 |
| k2 |
| 2 |
| k |
AB的垂直平分线MP的方程为y-
| 2 |
| k |
| 1 |
| k |
| k2+2 |
| k2 |
令y=0可得,x=3+
| 2 |
| k2 |
| 2 |
| k2 |
∴|MF1|=2+
| 2 |
| k2 |
∵|AB|=
| (x1-x2)2+(y1-y2)2 |
| (1+k2)[(x1+x2)2-4x1x2] |
=
(1+k2)[
|
| 4 |
| k2 |
∴
| |AB| |
| |MF1| |
(III)过圆锥曲线E的焦点F作与焦点所在的对称轴不垂直的任意直线L交于A,B两点,线段AB的垂直平分线交焦点所在的对称轴于点M,则
| |AB| |
| |MF| |
| 2 |
| e |
(法二)由题意可设双曲线C的方程为
| x2 |
| a2 |
| y2 |
| b2 |
由已知可得
|
解可得,
|
∴双曲线的方程为
| x2 |
| 3 |
(II ),(III)同法一

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 ,且点Q在x轴上的射影恰为该双曲线的一个焦点F1
,且点Q在x轴上的射影恰为该双曲线的一个焦点F1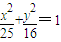 的一个焦点F作与x轴不垂直的任意直线l”交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F作与x轴不垂直的任意直线l”交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则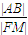 为定值,且定值是
为定值,且定值是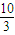 ”.命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F、M两点间距离的比值.试类比上述命题,写出一个关于抛物线C的类似的正确命题,并加以证明
”.命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F、M两点间距离的比值.试类比上述命题,写出一个关于抛物线C的类似的正确命题,并加以证明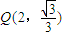 ,且点Q在x轴上的射影恰为该双曲线的一个焦点F1
,且点Q在x轴上的射影恰为该双曲线的一个焦点F1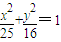 的一个焦点F作与x轴不垂直的任意直线l”交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F作与x轴不垂直的任意直线l”交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则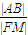 为定值,且定值是
为定值,且定值是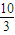 ”.命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F、M两点间距离的比值.试类比上述命题,写出一个关于抛物线C的类似的正确命题,并加以证明
”.命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F、M两点间距离的比值.试类比上述命题,写出一个关于抛物线C的类似的正确命题,并加以证明