摘要:(I)假设方程有异于的实根m.即.则有 成立 . 因为.所以必有.但这与≠1矛盾. 因此方程不存在异于c1的实数根. ∴方程只有一个实数根. (II)令. ∴函数为减函数. 又. ∴当时..即成立. (III)不妨设.为增函数. 即.又.∴函数为减函数 即. . 即. . .
网址:http://m.1010jiajiao.com/timu3_id_520901[举报]
 是定义在
是定义在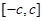 上的奇函数,其图象如图所示,令
上的奇函数,其图象如图所示,令 ,则下列关于函数
,则下列关于函数 的叙述正确的是()
的叙述正确的是()
A.若 ,则函数 ,则函数 的图象关于原点对称 的图象关于原点对称 |
B.若 ,则方程 ,则方程 有大于2的实根 有大于2的实根 |
C.若 ,则方程 ,则方程 有两个实根 有两个实根 |
D.若 ,则方程 ,则方程 有两个实根 有两个实根 |
 是定义在
是定义在 上的奇函数,其图象如图所示,令
上的奇函数,其图象如图所示,令 ,则下列关于函数
,则下列关于函数 的叙述正确的是()
的叙述正确的是()
A.若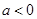 ,则函数 ,则函数 的图象关于原点对称 的图象关于原点对称 |
B.若 ,则方程 ,则方程 有大于2的实根 有大于2的实根 |
C.若 ,则方程 ,则方程 有两个实根 有两个实根 |
D.若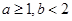 ,则方程 ,则方程 有两个实根 有两个实根 |
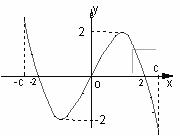
![]() 是定义在区间[-c,c]上的奇函数,其图象如图所示:令
是定义在区间[-c,c]上的奇函数,其图象如图所示:令![]() ,则下列关于函数
,则下列关于函数![]() 的叙述正确的是
的叙述正确的是
A.若![]() ,则函数
,则函数![]() 的图象关于原点对称
的图象关于原点对称
B![]() 若
若![]() ,则方程
,则方程![]() 有大于2的实根
有大于2的实根
C![]() 若
若![]() ,则方程
,则方程![]() 有两个实根
有两个实根
D![]()
![]() ,则方程
,则方程![]() 有三个实根
有三个实根