题目内容
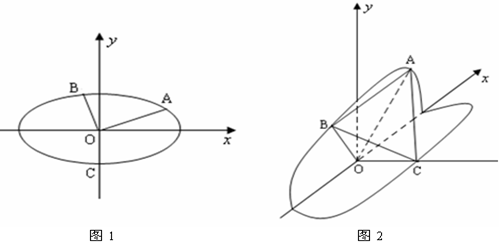
如图1,椭圆
+
=1的下顶点为C,A,B分别在椭圆的第一象限和第二象限的弧上运动,满足
⊥
,其中O为坐标原点,现沿x轴将坐标平面折成直二面角.如图2所示,在空间中,解答下列问题:
(1)证明:OC⊥AB;
(2)设二面角O-BC-A的平面角为α,二面角O-AC-B的平面角为β,二面角O-AB-C的平面角为θ,求证:cos2α+cos2β+cos2θ=1;
(3)求三棱锥O-ABC的体积的最小值.
| x2 |
| 9 |
| y2 |
| 4 |
| OA |
| OB |
(1)证明:OC⊥AB;
(2)设二面角O-BC-A的平面角为α,二面角O-AC-B的平面角为β,二面角O-AB-C的平面角为θ,求证:cos2α+cos2β+cos2θ=1;
(3)求三棱锥O-ABC的体积的最小值.

分析:(1)由题设知,沿x轴将坐标平面折成直二面角后,OC⊥x轴,且OC⊥y轴,所以OC⊥面AOB,由此能够证明OC⊥AB.
(2)由
⊥
,OA⊥OB,设直线OA方程为y=kx,OB的方程为y=-
,解方程组
,得A(
,
),解方程组
,得B(-
,
),OA=
,OB=
,OC=2,以O为原点,以OA为x轴,OB为y轴,OC为z轴,建立空间直角坐标系,由向量法能够证明cos2α+cos2β+cos2θ=1.
(3)由OC⊥面OAB,知三棱锥O-ABC的高OC=2,底面积S=S△0AB=
×
×
=
≥3,由此能求出三棱锥O-ABC的体积的最小值.
(2)由
| OA |
| OB |
| x |
| k |
|
| 6 | ||
|
| 6k | ||
|
|
| 6k | ||
|
| 6 | ||
|
6
| ||
|
6
| ||
|
(3)由OC⊥面OAB,知三棱锥O-ABC的高OC=2,底面积S=S△0AB=
| 1 |
| 2 |
6
| ||
|
6
| ||
|
| 18(1+k2) | ||
|
解答:(1)证明:由题设知,沿x轴将坐标平面折成直二面角后,
∵OC⊥x轴,且OC⊥y轴,
∴OC⊥面AOB,
∵AB?面AOB,
∴OC⊥AB.
(2)证明:∵
⊥
,∴OA⊥OB,
∴设直线OA方程为y=kx,OB的方程为y=-
,
解方程组
,得A(
,
),(舍去x<0的解)
解方程组
,得B(-
,
),(舍去x>0的解)
∵O(0,0),
∴OA=
,OB=
,OC=2,
∵OC⊥面AOB,OA⊥OB,
∴以O为原点,以OA为x轴,OB为y轴,OC为z轴,建立空间直角坐标系,
则A(
,0,0),B(0,
,0),C(0,0,2),
∴
=(
,0,-2),
=(0,
,0),
设平面ABC的法向量
=(x,y,z),则有
,
∴
=(1,
,0),
∵平面OBC的法向量
=(1,0,0),
∴cosα=cos<
,
>=
,
∵平面OAC的法向量
=(0,1,0),
∴cosβ=
,
∵平面OAB的法向量
=(0,0,1),
∴cosθ=
,
∴cos2α+cos2β+cos2θ=
+
=1.
(3)解:∵OC⊥面OAB,
∴三棱锥O-ABC的高OC=2,
底面积S=S△0AB=
×
×
=
≥3,
当且仅当k=0时,取最小值.
∴三棱锥O-ABC的体积的最小值Vmin=
×3×2=2.
∵OC⊥x轴,且OC⊥y轴,
∴OC⊥面AOB,
∵AB?面AOB,
∴OC⊥AB.
(2)证明:∵
| OA |
| OB |
∴设直线OA方程为y=kx,OB的方程为y=-
| x |
| k |
解方程组
|
| 6 | ||
|
| 6k | ||
|
解方程组
|
| 6k | ||
|
| 6 | ||
|
∵O(0,0),
∴OA=
6
| ||
|
6
| ||
|
∵OC⊥面AOB,OA⊥OB,
∴以O为原点,以OA为x轴,OB为y轴,OC为z轴,建立空间直角坐标系,
则A(
6
| ||
|
6
| ||
|
∴
| CA |
6
| ||
|
| CB |
6
| ||
|
设平面ABC的法向量
| n |
|
∴
| n |
| ||
|
∵平面OBC的法向量
| n1 |
∴cosα=cos<
| n |
| n1 |
| 1 | ||||
|
∵平面OAC的法向量
| n2 |
∴cosβ=
| ||||||
|
∵平面OAB的法向量
| n3 |
∴cosθ=
| 0 | ||||
|
∴cos2α+cos2β+cos2θ=
| 1 | ||
1+
|
| ||
1+
|
(3)解:∵OC⊥面OAB,
∴三棱锥O-ABC的高OC=2,
底面积S=S△0AB=
| 1 |
| 2 |
6
| ||
|
6
| ||
|
| 18(1+k2) | ||
|
当且仅当k=0时,取最小值.
∴三棱锥O-ABC的体积的最小值Vmin=
| 1 |
| 3 |
点评:本题考查直线与圆锥曲线的综合应用,难度大,综合性强,易出错.解题时巧妙地引空间直角坐标系,恰当地利用空间向量进行求解,能够简化运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
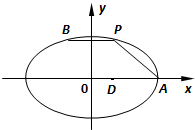 (2012•盐城一模)如图,在平面直角坐标系xoy中,已知点A为椭圆
(2012•盐城一模)如图,在平面直角坐标系xoy中,已知点A为椭圆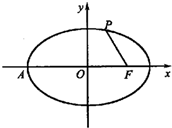 (文)如图点P为椭圆
(文)如图点P为椭圆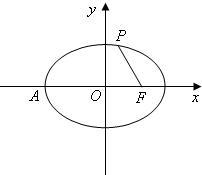 如图,点P为椭圆
如图,点P为椭圆 如图,M为椭圆
如图,M为椭圆