摘要:例4.过正方形的顶点A.引.若. 则平面与平面所成的二面角的大小. 解:以为原点.分别为轴轴,轴建立空间直角坐标系如图. 则. . , ,则..设平面PCD的法向量为,,即,.即.所以可令,设平面PAB的法向量为.所以平面PAB与平面PCD所成的二面角的余弦值为.所以平面与平面所成的二面角的平面角为. 既然可以利用两个平面的法向量求两平面的夹角.也可以利用两个平面法向量证明两平面垂直.如下面的例5.可以先求两平面的法向量.再计算它们的数量积. 例5.如图.正四棱柱中.底面边长为.侧棱长为4.分别为棱的中点. 求证:平面平面 解:以为原点.分别 为建立空间直角坐标系.则. . ,, 设平面EF的法向量为. 则=0,即.所以令= 设平面的法向量为=,,即4=0; ,即.所以可令. =0 平面平面.
网址:http://m.1010jiajiao.com/timu3_id_520231[举报]
 的顶点
的顶点 ,引
,引 ⊥平面
⊥平面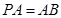 ,则平面ABCD和平面
,则平面ABCD和平面 所成的二面角的大小是
所成的二面角的大小是