摘要: 解: ,则该圆的方程为(x-m)2+(y-n)2=8已知该圆与直线y=x相切.那么圆心到该直线的距离等于圆的半径.则 =2 即=4 ① 又圆与直线切于原点.将点(0.0)代入得 m2+n2=8 ② 联立方程①和②组成方程组解得 故圆的方程为(x+2)2+(y-2)2=8 (2)=5.∴a2=25.则椭圆的方程为 + =1 其焦距c==4.右焦点为(4.0).那么=4. 要探求是否存在异于原点的点Q.使得该点到右焦点F的距离等于的长度4.我们可以转化为探求以右焦点F为顶点.半径为4的圆2+y2=8与(1)所求的圆的交点数. 通过联立两圆的方程解得x=.y= 即存在异于原点的点Q(.).使得该点到右焦点F的距离等于的长. 广东文
网址:http://m.1010jiajiao.com/timu3_id_519685[举报]
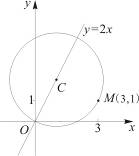
求圆心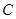 在直线
在直线 上,且经过原点及点
上,且经过原点及点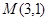 的圆
的圆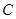 的标准方程.
的标准方程.
【解析】本试题主要考查的圆的方程的求解,利用圆心和半径表示圆,首先设圆心C的坐标为( ),然后利用
),然后利用 ,得到
,得到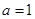 ,从而圆心
,从而圆心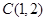 ,半径
,半径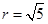 .可得原点 标准方程。
.可得原点 标准方程。
解:设圆心C的坐标为( ),...........2分
),...........2分
则 ,即
,即
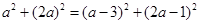 ,解得
,解得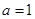 ........4分
........4分
所以圆心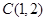 ,半径
,半径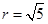 ...........8分
...........8分
故圆C的标准方程为: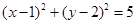 .......10分
.......10分
查看习题详情和答案>>
选做题(请在下列2道题中任选一题作答,如果多做,则按所做的第一题评阅记分)
A.不等式|x+1|+|x-2|≤5的解集为 .
B.直线
,(t为参数)过圆x2+y2-2ax+ay+
a2-1=0的圆心,则圆心坐标为 .
查看习题详情和答案>>
A.不等式|x+1|+|x-2|≤5的解集为
B.直线
|
| 5 |
| 4 |
 选做题(请在下列3道题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请在下列3道题中任选一题作答,如果多做,则按所做的第一题评阅记分)