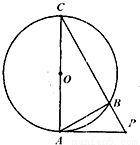题目内容
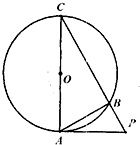 选做题(请在下列3道题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请在下列3道题中任选一题作答,如果多做,则按所做的第一题评阅记分)A.不等式|x+1|+|x-2|≤4的解集为
B.直线
|
| 5 |
| 4 |
则圆心坐标为
C.已知PA是⊙O的切线,切点为A,PA=2cm,AC是⊙O的直径,PC交⊙O于点B,AB=
| 3 |
分析:A.根据绝对值的几何意义直接求出不等式|x+1|+|x-2|≤4的解集即可;
B.求出圆x2+y2-2ax+ay+
a2-1=0的圆心,代入直线
,(t为参数),求出a,然后求出圆心坐标.
C.求出PB,利用射影定理,求出BC,然后求出△ABC的面积.
B.求出圆x2+y2-2ax+ay+
| 5 |
| 4 |
|
C.求出PB,利用射影定理,求出BC,然后求出△ABC的面积.
解答:解:A.由绝对值的几何意义可知不等式|x+1|+|x-2|≤4的解集为[-
,
].
B.圆x2+y2-2ax+ay+
a2-1=0的圆心(a,-
),代入直线
,(t为参数),
,a=
,所以圆心坐标为 (
,-
).
C.已知PA是⊙O的切线,切点为A,PA=2cm,AC是⊙O的直径,PC交⊙O于点B,AB=
cm,所以PB=1,由射影定理可知,BC=3,则△ABC的面积为
cm2.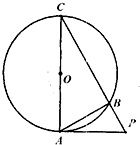
故答案为:[-
,
];(
,-
);
| 3 |
| 2 |
| 5 |
| 2 |
B.圆x2+y2-2ax+ay+
| 5 |
| 4 |
| a |
| 2 |
|
|
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
C.已知PA是⊙O的切线,切点为A,PA=2cm,AC是⊙O的直径,PC交⊙O于点B,AB=
| 3 |
| 3 |
| 2 |
| 3 |
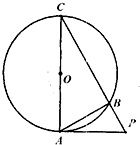
故答案为:[-
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
点评:本题是基础题,A考查绝对值的几何意义;B考查直线的参数方程,含变量的圆的方程;C射影定理的应用,考查计算能力.

练习册系列答案
相关题目
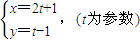 过圆
过圆 的圆心,
的圆心,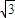 cm,则△ABC的面积为 cm2.
cm,则△ABC的面积为 cm2.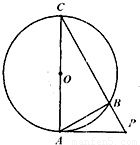
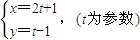 过圆
过圆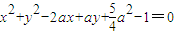 的圆心,
的圆心,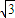 cm,则△ABC的面积为 cm2.
cm,则△ABC的面积为 cm2.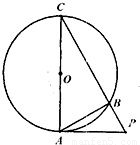
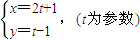 过圆
过圆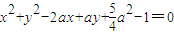 的圆心,
的圆心,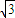 cm,则△ABC的面积为 cm2.
cm,则△ABC的面积为 cm2.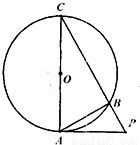
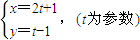 过圆
过圆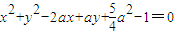 的圆心,
的圆心,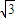 cm,则△ABC的面积为 cm2.
cm,则△ABC的面积为 cm2.