摘要:对于在区间[m.n]上有意义的两个函数f (x)与g (x).如果对任意x∈[m.n]均有| f (x) – g (x) |≤1.则称f (x)与g (x)在[m.n]上是接近的.否则称f (x)与g (x)在[m.n]上是非接近的.现有两个函数f 1(x) = loga(x – 3a)与f 2 (x) = loga(a > 0.a≠1).给定区间[a + 2.a + 3]. (1)若f 1(x)与f 2 (x)在给定区间[a + 2.a + 3]上都有意义.求a的取值范围, (2)讨论f 1(x)与f 2 (x)在给定区间[a + 2.a + 3]上是否是接近的? 解:(1)要使f 1 (x)与f 2 (x)有意义.则有 要使f 1 (x)与f 2 (x)在给定区间[a + 2.a + 3]上有意义. 等价于真数的最小值大于0 即 (2)f 1 (x)与f 2 (x)在给定区间[a + 2.a + 3]上是接近的 | f 1 (x) – f 2 (x)|≤1 ≤1 |loga[(x – 3a)(x – a)]|≤1 a≤(x – 2a)2 – a2≤ 对于任意x∈[a + 2.a + 3]恒成立 设h(x) = (x – 2a)2 – a2.x∈[a + 2.a + 3] 且其对称轴x = 2a < 2在区间[a + 2.a + 3]的左边 当时 f 1 (x)与f 2 (x)在给定区间[a + 2.a + 3]上是接近的 当< a < 1时.f 1 (x)与f 2 (x)在给定区间[a + 2.a + 3]上是非接近的.
网址:http://m.1010jiajiao.com/timu3_id_519407[举报]
对于在区间[m,n]上有意义的两个函数f(x)与g(x),如果对任意的x∈[m,n],均有|f(x)-g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的,否则称f(x)与g(x)在[m,n]上是非接近的.现有两个函数f1(x)=loga(x-2a)与f2(x)=loga
,(a>0,且a≠1),给定区间[a+1,a+2]
(1)若f1(x)与f2(x)在区间[a+1,a+2]上都有意义,求a的取值范围;
(2)在(1)的条件下,讨论f1(x)与f2(x)在区间[a+1,a+2]上是否是接近的.
查看习题详情和答案>>
| 1 | x-a |
(1)若f1(x)与f2(x)在区间[a+1,a+2]上都有意义,求a的取值范围;
(2)在(1)的条件下,讨论f1(x)与f2(x)在区间[a+1,a+2]上是否是接近的.
对于在区间[m,n]上有意义的两个函数f(x)与g(x),如果对于任意的x∈[m,n],均有|f(x)-g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的,若函数f(x)=x2-2x+3与g(x)=3x-2在区间[m,n]上是接近的,给出如下区间:(1)[1,4](2)[1,2](3)[1,2]∪[3,4](4) ,则区间[m,n]可以是 (把你认为正确的序号都填上)
查看习题详情和答案>>
,则区间[m,n]可以是 (把你认为正确的序号都填上)
查看习题详情和答案>>
 ,则区间[m,n]可以是 (把你认为正确的序号都填上)
查看习题详情和答案>>
,则区间[m,n]可以是 (把你认为正确的序号都填上)
查看习题详情和答案>>
对于在区间 [ m,n ] 上有意义的两个函数 与
与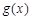 ,如果对任意
,如果对任意 ,均有
,均有 ,则称
,则称 与
与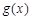 在 [ m,n ] 上是友好的,否则称
在 [ m,n ] 上是友好的,否则称 与
与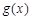 在 [ m,n ]是不友好的.现有两个函数
在 [ m,n ]是不友好的.现有两个函数 与
与 (a > 0且
(a > 0且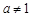 ),给定区间
),给定区间 .
.
(1)若 与
与 在给定区间
在给定区间 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;
(2)讨论 与
与 在给定区间
在给定区间 上是否友好.
上是否友好.
查看习题详情和答案>>
 与
与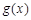 ,如果对任意
,如果对任意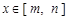 ,均有
,均有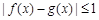 ,则称
,则称 与
与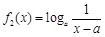 (a > 0且
(a > 0且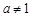 ),给定区间
),给定区间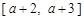 .
. 与
与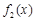 在给定区间
在给定区间 与
与 ,如果对任意
,如果对任意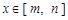 ,均有
,均有 与
与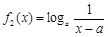 (a > 0且
(a > 0且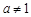 ),给定区间
),给定区间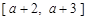 .
.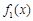 与
与 在给定区间
在给定区间