题目内容
对于在区间[m,n]上有意义的两个函数f(x)与g(x),如果对任意的x∈[m,n],均有|f(x)-g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的,否则称f(x)与g(x)在[m,n]上是非接近的.现有两个函数f1(x)=loga(x-2a)与f2(x)=loga
,(a>0,且a≠1),给定区间[a+1,a+2]
(1)若f1(x)与f2(x)在区间[a+1,a+2]上都有意义,求a的取值范围;
(2)在(1)的条件下,讨论f1(x)与f2(x)在区间[a+1,a+2]上是否是接近的.
| 1 | x-a |
(1)若f1(x)与f2(x)在区间[a+1,a+2]上都有意义,求a的取值范围;
(2)在(1)的条件下,讨论f1(x)与f2(x)在区间[a+1,a+2]上是否是接近的.
分析:(1)根据f1(x)与f2(x)在区间[a+1,a+2]上都有意义,利用对数函数成立的条件即可求a的取值范围;
(2)根据函数接近的定义进行判断即可.
(2)根据函数接近的定义进行判断即可.
解答:解:(1)若f1(x)与f2(x)在区间[a+1,a+2]上都有意义,
则
,即
,
∴0<a<1
∴a的取值范围是(0,1).
(2)设m(x)=f1(x)-f2(x)=loga(x-2a)-loga
=loga[(x-2a)(x-a)],
若m(x)=f1(x)-f2(x)在区间[a+1,a+2]上是接近的,
则|loga[(x-2a)(x-a)]|≤1,即a≤(x-2a)(x-a)≤
,
∵0<a<1
∴a<2a<a+1<a+2,
∴y=(x-2a)(x-a)在[a+1,a+2]上单调递增,ymax=4-2a,ymin=1-a,
∴满足
,
即
,
∴0<a≤
,
即当0<a≤
时,f1(x)与f2(x)在区间[a+1,a+2]上是接近的,
当
<a<1时,f1(x)与f2(x)在区间[a+1,a+2]上不接近.
则
|
|
∴0<a<1
∴a的取值范围是(0,1).
(2)设m(x)=f1(x)-f2(x)=loga(x-2a)-loga
| 1 |
| x-a |
若m(x)=f1(x)-f2(x)在区间[a+1,a+2]上是接近的,
则|loga[(x-2a)(x-a)]|≤1,即a≤(x-2a)(x-a)≤
| 1 |
| a |
∵0<a<1
∴a<2a<a+1<a+2,
∴y=(x-2a)(x-a)在[a+1,a+2]上单调递增,ymax=4-2a,ymin=1-a,
∴满足
|
即
|
∴0<a≤
2-
| ||
| 2 |
即当0<a≤
2-
| ||
| 2 |
当
2-
| ||
| 2 |
点评:本题考查对数函数的性质和应用,解题时要注意函数恒成立的充要条件的合理运用.综合性较强,难度较大.

练习册系列答案
相关题目
 与
与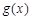 ,如果对任意
,如果对任意 ,均有
,均有 与
与 (a > 0且
(a > 0且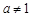 ),给定区间
),给定区间 .
. 与
与 在给定区间
在给定区间