摘要:19.已知f(x)是定义在[-1.1]上的奇函数.且f (1)=1.若m.n∈[-1.1].m+n≠0时有 (1)判断f (x)在[-1.1]上的单调性.并证明你的结论, (2)解不等式:, (3)若f (x)≤对所有x∈[-1.1].∈[-1.1]恒成立.求实数t的取值范围. 解:(1)任取-1≤x1<x2≤1.则 f (x1)-f (x2)= f (x1)+f (-x2)= ∵-1≤x1<x2≤1.∴x1+(-x2)≠0. 由已知>0.又x1-x2<0. ∴f (x1)-f (x2)<0.即f (x)在[-1.1]上为增函数. (2)∵f (x)在[-1.1]上为增函数.故有 可知:f(x)在[-1.1]上是增函数.且f (1)=1.故对x∈[-l.1].恒有f(x)≤1. 所以要使f(x)≤.对所有x∈[-1.1]. ∈[-1.1]恒成立. 即要≥1成立.故≥0成立. 记g()=对 ∈[-1.1].g()≥0恒成立.只需g()在[-1.1]上的最小值 大于等于零. 故解得:t≤-2或t=0.或
网址:http://m.1010jiajiao.com/timu3_id_518957[举报]
已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若m,n∈[-1,1],m+n≠0时, ,
,
(Ⅰ)用定义证明:f(x)在[-1,1]上是增函数;
(Ⅱ)解不等式: ;
;
(Ⅲ)若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围。
查看习题详情和答案>>
 ,
,(Ⅰ)用定义证明:f(x)在[-1,1]上是增函数;
(Ⅱ)解不等式:
 ;
;(Ⅲ)若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围。
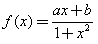 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且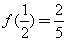 。
。