题目内容
已知f (x)是定义在[ 4，4]上的奇函数，在[0，4]单调递增，且
，f (x + 1) = f (x) + f (1)，设f (x)的反函数是
，则
= ；f (x)的值域为 .
4, [2，2]
解析：由题设知f (0) = 0，f (4) = 2，f ( 4) = 2，∴
，又f (x)在[0，4]递增，∴f (x)在[ 4，4]上递增，∴f (x)的值域为[2，2].
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
)x，那么f-1(0)+f-1(-8)的值为( )
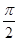)∪(0,1)∪(