摘要:9..如图.平面α⊥平面β.A∈α.B∈β.AB与两平面α.β所成的角分别为和.过A.B分别作两平面交线的垂线.垂足为A′.B′.则AB∶A′B′= (A)2∶1 (B)3∶1 (C)3∶2 (D)4∶3 解析:连接,设AB=a,可得AB与平面所成的角为 ,在,同理可得AB与平面所成的角为,所以,因此在,所以,故选A [典型考例] 例1.(P75例3) 如图.在五面体ABCDEF中.点O是矩形ABCD的对角线的交点.面CDE是等边三角形.棱 (I)证明平面 (II)设证明平面 (19)本小题考查直线与平面平行.直线与平面垂直等基础知识.考查空间想象能力和推理论证能力.满分12分. (I)证明:取CD中点M.连结OM. 在矩形ABCD中. 又 则连结EM.于是 四边形EFOM为平行四边形. 又平面CDE.且平面CDE.平面CDE. 和已知条件.在等边中. 且 因此平行四边形EFOM为菱形.从而. 平面EOM.从而 而所以平面 例2. 如图, 在直三棱柱ABC-A1B1C1中.AC=3.BC=4.AA1=4.AB=5点D是AB的中点. (I)求证:AC⊥BC1, (II)求证:AC 1//平面CDB1, (III)设BD1的中点为F.求三棱锥B1-BEF的体积 证:(I)直三棱柱ABC-A1B1C1.底面三边长AC=3.BC=4AB=5. ∴ AC⊥BC.且BC1在平面ABC内的射影为BC.∴ AC⊥BC1, (II)设CB1与C1B的交点为E.连结DE.∵ D是AB的中点.E是BC1的中点.∴ DE//AC1. ∵ DE平面CDB1.AC1平面CDB1.∴ AC1//平面CDB1, 例2.已知ABCD是上.下底边长分别为2和6.高为的等腰梯形.将它沿对称轴OO1折成直二面角 (Ⅰ)证明:AC⊥BO1, (Ⅱ)求点O1到平面AOC的距离. (III)求四面体O1-ACO的体积. (I)证明 由题设知OA⊥OO1.OB⊥OO1. 所以∠AOB是所折成的直二面角的平面角. 即OA⊥OB. 故可以O为原点.OA.OB.OO1 所在直线分别为轴.y轴.z轴建立空间直角坐标系. 如图3.则相关各点的坐标是A. B.C(0.1.)O1(0.0.). 从而 所以AC⊥BO1. 例3.如图.在底面为平行四边形的四棱锥中..平面.且.点是的中点.(Ⅰ)求证:,(Ⅱ)求证:平面, (Ⅲ)求四面体B-AED的体积. 解:(1)由平面可得PA^AC 又.所以AC^平面PAB.所以 (2)如图.连BD交AC于点O.连EO.则 EO是△PDB的中位线.\EOPB \PB平面 (3)如图.取AD的中点F.连EF.FO.则EF是△PAD的中位线.\EFPA又平面.\EF^平面 同理FO是△ADC的中位线.\FOAB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角.又FO=AB=PA=EF\ÐEOF=45°而二面角与二面角E-AC-D互补.故所求二面角的大小为135°. 例4.如图.已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为1.M是底面BC边上的中点.N是侧棱CC1上的点.(Ⅰ)当B1M⊥AN时.求CN的长度,(Ⅱ)若CN=时.求点B1到平面AMN的距离.
网址:http://m.1010jiajiao.com/timu3_id_517907[举报]
 如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,E为边BC上的动点.
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,E为边BC上的动点.(1)证明:无论点E在边BC的何处,都有PE⊥AF
(2)当BE等于何值时,二面角P-DE-A的大小为45°
(3)在(2)问的条件下,求P点到角AEF的距离.
 如图,在平面直角坐标系中,以Ox轴为始边作两锐角α,β,它们终边分别与单位圆交于A,B两点,且A,B横坐标分别为
如图,在平面直角坐标系中,以Ox轴为始边作两锐角α,β,它们终边分别与单位圆交于A,B两点,且A,B横坐标分别为| 7 |
| 10 |
| 2 |
| 3 |
| 10 |
| 10 |
(1)求tan∠AOB
(2)求α+2β的值.
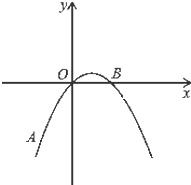 如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过点A(-2,-4),O(0,0),B(2,0).
如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过点A(-2,-4),O(0,0),B(2,0).(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.
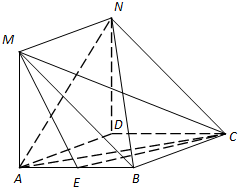 (2013•武汉模拟)如图,MA⊥平面ABCD,四边形ABCD是菱形,且四边形ADNM是平行四边形.
(2013•武汉模拟)如图,MA⊥平面ABCD,四边形ABCD是菱形,且四边形ADNM是平行四边形.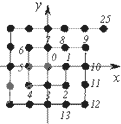 如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签;原点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,…,依此类推,则标签2013×2014对应的格点的坐标为
如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签;原点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,…,依此类推,则标签2013×2014对应的格点的坐标为