摘要:21.已知函数.记..且. (1)求数列的前项和, (2)解关于的不等式, (3)证明. [解答](1)∵. . -- . ∴. 而. ∴.∴. ∴ , (2)当时.成立.故是不等式的一个解. 当时.成立.故不是不等式的解. 当时.成立.故也不是不等式的解. 当.时.∵. ∴故.故.都是不等式的解. 综合知所求的解集为.且, (3)∵. 且由(2)知. ∴.
网址:http://m.1010jiajiao.com/timu3_id_517799[举报]
记数列{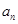 }的前n项和为为
}的前n项和为为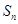 ,且
,且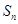 +
+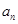 +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.
(1)求证:数列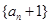 是等比数列;
是等比数列;
(2)已知2是函数f(x)=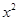 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥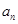 对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
查看习题详情和答案>>
已知函数 满足
满足 ,且
,且 有唯
有唯
一实数解。
(1)求 的表达式 ;
的表达式 ;
(2)记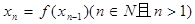 ,且
,且 =
=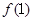 ,求数列
,求数列 的通项公式。
的通项公式。
(3)记  ,数列{
,数列{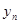 }的前
}的前  项和为
项和为
 ,是否存在k∈N*,使得
,是否存在k∈N*,使得
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
查看习题详情和答案>>
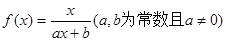 满足
满足 ,且
,且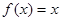 有唯
有唯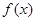 的表达式 ;
的表达式 ;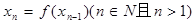 ,且
,且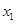 =
=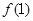 ,求数列
,求数列 的通项公式。
的通项公式。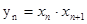 ,数列{
,数列{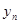 }的前
}的前 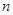 项和为
项和为
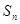 ,是否存在k∈N*,使得
,是否存在k∈N*,使得
 满足
满足 ,且
,且 有唯
有唯 的表达式 ;
的表达式 ; ,且
,且 =
= ,求数列
,求数列 的通项公式。
的通项公式。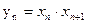 ,数列{
,数列{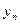 }的前
}的前  项和为
项和为  ,是否存在k∈N*,使得
,是否存在k∈N*,使得