题目内容
记数列{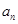 }的前n项和为为
}的前n项和为为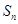 ,且
,且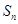 +
+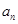 +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.
(1)求证:数列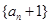 是等比数列;
是等比数列;
(2)已知2是函数f(x)=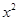 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥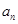 对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
【答案】
(Ⅰ)见解析;(II)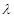 的取值范围
的取值范围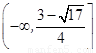 .
.
【解析】
试题分析:(Ⅰ)利用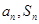 间的关系解答,写出
间的关系解答,写出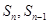 相减,然后根据等比数列定义确定答案;(II)利用(Ⅰ)的结果和等比数列通项公式求出
相减,然后根据等比数列定义确定答案;(II)利用(Ⅰ)的结果和等比数列通项公式求出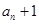 ,然后构造出不等式
,然后构造出不等式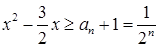 ,求出
,求出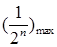 解关于
解关于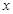 的不等式得出答案.
的不等式得出答案.
试题解析:(Ⅰ) 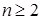 时,
时,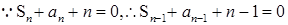 ,两式相减可得,
,两式相减可得,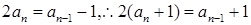 ,
,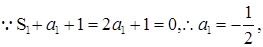
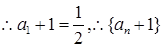 是以
是以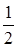 为首项,
为首项,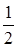 为公比的等比数列. 6分
为公比的等比数列. 6分
(II)由(Ⅰ)可得,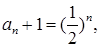
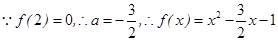 ,
,
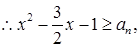 即
即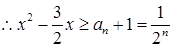 ,
,
即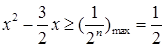 在
在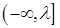 上恒成立,由
上恒成立,由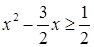 ,即
,即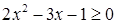 ,
,
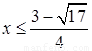 或
或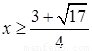 ,
,
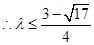 ,
,
即所求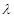 的取值范围
的取值范围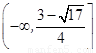 . 12分
. 12分
考点:等比数列定义和通项公式、函数最值、一元二次不等式解法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
