摘要:样本平均数 规律:kx1+m,kx2+m,-kxn+m的平均数为k+m.方差为k2S2. 20抽样方法:①简单随机抽样,②系统抽样,③分层抽样的各自特点及适用范围,它们的共同点都是等概率抽样.对于简单随机抽样的概念中.“每次抽取时的各个个体被抽到的概率相等 .如从含有N个个体的总体中.采用随机抽样法.抽取n个个体.则每个个体第一次被抽到的概率为.第二次被抽到的概率为.--故每个个体被抽到的概率为.即每个个体入样的概率为. 21体分布的估计 用样本去估计总体.用样本平均数估计总体平均数.用样本方差估计总体方差,平均数反映了一组数据的平均水平.而方差是描述一组数据的波动情况.即偏离平均数的大小.或者说数据的稳定性.
网址:http://m.1010jiajiao.com/timu3_id_517506[举报]
(2013•肇庆一模)甲、乙两种水稻试验品种连续5年的单位面积平均产量如下(单位:t/hm2),根据这组数据下列说法正确的是( )
|
查看习题详情和答案>>
 2013年1月份,我国北方部分城市出现雾霾天气,形成雾霾天气主要原因与PM2.5有关.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:
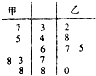
2013年1月份,我国北方部分城市出现雾霾天气,形成雾霾天气主要原因与PM2.5有关.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k<75 | 二级 |
| k>75 | 超标 |
(Ⅰ)分别求出甲、乙两市PM2.5日均值的样本平均数,并由此判断哪个市的空气质量较好;
(Ⅱ)若从甲市这6天的样本数据中随机抽取两天的数据,求恰有一天空气质量超标的概率.
 (2012•潍坊二模)PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.2012年2月29日,国家环保部发布了新修订的《环境空气质量标准》,其中空气质量等级标准见下表:
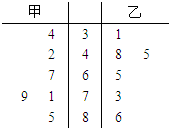
(2012•潍坊二模)PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.2012年2月29日,国家环保部发布了新修订的《环境空气质量标准》,其中空气质量等级标准见下表:某环保部门为了解近期甲、乙两居民区的空气质量状况,在过去30天中分别随机抽测了5天的PM2.5日均值作为样本,样本数据如茎叶图所示(十位为茎,个位为叶).
(I)分别求出甲、乙两居民区PM2.5日均值的样本平均数,并由此判断哪个小区的空气质量较好一些;
(II)若从甲居民区这5天的样本数据中随机抽取两天的数据,求恰有一天空气质量超标的概率.
| PM2.5日均值k(微克) | 空气质量等级 |
| K≤35 | 一级 |
| 35<k≤75 | 二级 |
| K>75 | 超标 |