摘要:17.(本题共12分.第①小题4分.第②小题4分.第③小题4分) 已知f(x)=2sin(x+)cos (x+)+2cos2(x+)- ①求f(x)的最小正周期 ②若0≤≤求使f(x)为偶函数的的值. ③在②条件下.求满足f(x)=1, x∈[-]的x的集合.
网址:http://m.1010jiajiao.com/timu3_id_517257[举报]
(本题共2小题,第一小题4分,第二小题8分,共12分)
在学习二项式定理时,我们知道杨辉三角中的数具有两个性质:① 每一行中的二项式系数是“对称”的,即第1项与最后一项的二项式系数相等,第2项与倒数第2项的二项式系数相等,![]() ;② 图中每行两端都是1,而且除1以外的每一个数都等于它肩上两个数的和.我们也知道,性质①对应于组合数的一个性质:
;② 图中每行两端都是1,而且除1以外的每一个数都等于它肩上两个数的和.我们也知道,性质①对应于组合数的一个性质:![]() .
.
(1)试写出性质②所对应的组合数的另一个性质;
(2)请利用组合数的计算公式对(1)中组合数的另一个性质作出证明.
查看习题详情和答案>>(本小题满分12分)某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入为50万元.设 表示前
表示前 年的纯利润总和,
年的纯利润总和,  表示前
表示前 年的总支出.
年的总支出.
[ 前
前 年的总收入-前
年的总收入-前 年的总支出-投资额].
年的总支出-投资额].
(1)写出 的关系式
的关系式
(2) 写出前 年的纯利润总和
年的纯利润总和 关于
关于 的函数关系式;并求该厂从第几年开始盈利?
的函数关系式;并求该厂从第几年开始盈利?
(3)若干年后,投资商为开发新项目,对该厂有两种处理方案:①年平均纯利润达到最大时,以48万元出售该厂;②纯利润总和达到最大时,以16万元万元出售该厂,问哪种方案更合算?
查看习题详情和答案>>
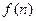 表示前
表示前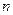 年的纯利润总和,
年的纯利润总和, 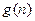 表示前
表示前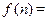 前
前