摘要: . 设数列前项和为,且(3,其中m为常数,m (1) 求证:是等比数列; (2) 若数列的公比q=f(m),数列满足求证:为等差数列,求.
网址:http://m.1010jiajiao.com/timu3_id_517218[举报]
(本小题满分14分)
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的n  N+,都有
N+,都有 。
。
(1)写出数列{an}的前3项;
(2)求数列{an}的通项公式(写出推证过程);
(3)设 ,
, 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得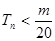 对所有n
对所有n  N+都成立的最小正整数
N+都成立的最小正整数 的值。
的值。
查看习题详情和答案>>
(本小题满分14分,第Ⅰ小题5分,第Ⅱ小题4分,第Ⅲ小题5分).
数列![]() 的各项均为正数,
的各项均为正数,![]() 为其前
为其前![]() 项和,对于任意
项和,对于任意![]() ,总有
,总有![]() 成等差数列.
成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,求证:对任意实数
,求证:对任意实数![]() (
(![]() 是常数,
是常数,![]() =2.71828
=2.71828![]() )和任意正整数
)和任意正整数![]() ,总有
,总有![]()
![]() 2;
2;
(Ⅲ) 正数数列![]() 中,
中,![]() .求数列
.求数列![]() 中的最大项.
中的最大项.
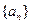 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且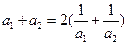 ,
,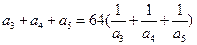
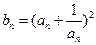 ,求数列
,求数列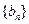 的前
的前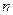 项和
项和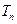 。
。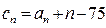 ,求数列{
,求数列{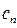 }的前
}的前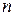 项和最小时
项和最小时 的图象经过坐标原点,与
的图象经过坐标原点,与 轴的另一个交点为
轴的另一个交点为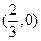 ,且
,且 ,数列
,数列 的前
的前 项的和为
项的和为 ,点
,点 在函数
在函数 ,求数列
,求数列 的前
的前 .
.