摘要:2.如图.已知△ABC是边长为1的正三角形.点D.E分别是边AB.AC上的点.线段DE经过△ABC的中心G..(0<m1,0<n1). (1)求证:=3 (2)求△ADE的面积的最小值和最大值. 解:(1)如图延长AG交BC与F.G为△ABC的中心 F为BC的中点.则有 .. 即 D.G.E三点共线 故=3 (2)△ABC是边长为1的正三角形 . S=mn 由=3.0<m1,0<n1 n=, 即. S=mn= 设t=m-则m=t+() S=mn=(t++) 易知在为减函数.在为增函数. t=时.取得最小值.即S取得最小值 又.取得最大值是.则S取得最大值
网址:http://m.1010jiajiao.com/timu3_id_516851[举报]
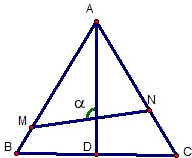 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a(| π |
| 3 |
| 2π |
| 3 |
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数.
(2)求y=
| 1 |
| S12 |
| 1 |
| S22 |
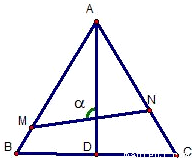 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(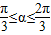 )
)(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数.
(2)求y=
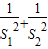 的最大值与最小值.
的最大值与最小值.查看习题详情和答案>>
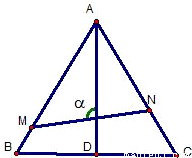 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(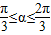 )
)(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数.
(2)求y=
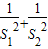 的最大值与最小值.
的最大值与最小值.查看习题详情和答案>>
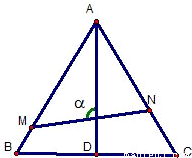 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(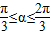 )
)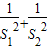 的最大值与最小值.
的最大值与最小值. 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a( )
) 的最大值与最小值.
的最大值与最小值.